Digital Signal Processing Reference
In-Depth Information
This result can be generalized to the sum of
N
independent Poisson random
variables,
X ¼
X
N
X
i
;
(5.166)
i¼
1
where
X ¼ k ¼
X
X
i
¼
X
N
N
k
i
:
(5.167)
i¼
1
i¼
1
According to the central limit theorem, the probabilities (
5.149
) for the sum
(
5.166
) approximate Gaussian PDF curve. Consequently, if the Poisson random
variable has a large mean value (
5.167
), this value can be considered to be a sum of
a large number of corresponding mean values, as shown in (
5.167
). Taking this
case, the probability (
5.149
) of a Poisson random variable can be computed using
formulas from Chapter 4.2.2.
5.7.6 Poisson Flow of Events
A sequence of homogeneous events occurring one after another at random moments
is called a
flow of events
or
calls
. Graphically, it can be presented as a set of points
on time axis, as shown in Fig.
5.17
.
The flow is called
ordinary
, if the probability of the occurrence of more than one
event in the elementary interval
Dt
is negligibly small compared to the probability
of the occurrence of only one event. In a
stationary flow
, the probability that a
certain number of events occurs in a given time interval depends only on the length
of the time interval and is independent on the position of this interval on the time
axis. In this case, the average number of events
l
occurring per unit of time—called
intensity of flow
—is constant. If the number of events occurring in one interval of
time does not depend on the number of events falling in any other nonoverlapping
interval, the flow is said to be
without aftereffects
.
A stationary flow of events which is ordinary and without aftereffects is called an
elementary
or
Poisson flow
.
Next we show that the probability that
k
events occur in an arbitrary time interval
t
of a Poisson flow is described using Poisson formula (
5.149
).
Fig. 5.17
Flow of events
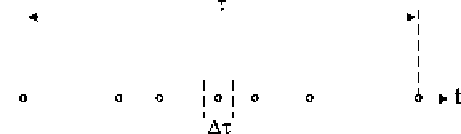



Search WWH ::

Custom Search