Multidimensional Random Variables - Random Signals and Processes Primer with MATLAB - page 178

Fig. 3.9 Linear dependency

The covariance is equal to:

C X 1 X 2 ¼ ðX 1 X 1 ÞðaX 1 þ b aX 1 þ bÞ¼ðX 1 X 1 ÞaðX 1 X 1 Þ
¼ aðX 1 X 1 Þ

2

¼ as X 1 : (3.133)

From ( 2.355 ) , the variance of the random variable X 2 is

s X 2 ¼ a 2 s X 1 : (3.134)

Finally, using ( 3.133 ) and ( 3.134 ), we can obtain the correlation coefficient:

as X 1

C X 1 X 2 a

jaj ¼

1 for a > 0

r X 1 X 2 ¼

s X 1 s X 2 ¼ s X 1 jajs X 1 ¼

: (3.135)

1 for a < 0

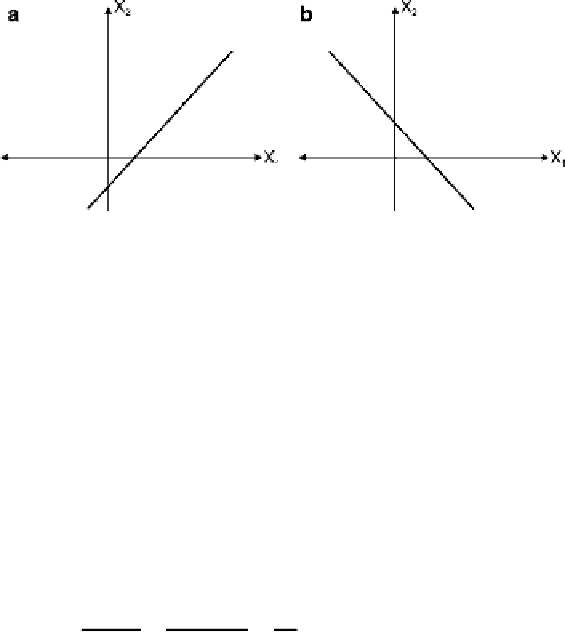
Therefore, the maximum absolute value of the correlation coefficient is equal
to 1 ( if the variables are linearly dependent ), as given in ( 3.135 ).
If

r X 1 X 2 > 0 ; (3.136)

then there is a positive correlation , as shown in Fig. 3.10a , in contrast, to the case
in which

r X 1 X 2 < 0 ; (3.137)

there is a negative correlation .
Note that in ( 3.136 ) and ( 3.137 ) there is no functional relation between variables,
but only tendency: if one variable increases, in the majority of cases, the other
variable either increases (positive correlation) or decreases (negative correlation).
Therefore, the coefficient of correlation presents the degree of linear dependency.
If there is no linear dependency between the variables (like in Fig. 3.11a ) the
coefficient of correlation is equal to zero. As a consequence, the random variables
are dependent, but uncorrelated.