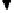Geoscience Reference
In-Depth Information
4
Ê
ˆ
1
Â
zz
-
Á
˜
i
j
2
Nh
()
.
Ë
¯
Nh
()
ˆ
()
g
h
=
(14.2)
0 457
+
.
()
0 494
Nh
This modified form of the variogram has the advantage of reducing the effect of outliers in the
data without removing specific data points. The estimation is based on the fourth power of the
square root of the absolute differences in
-values.
Once an appropriate empirical variogram is calculated, a model is fit to the data (Figure 14.1).
The model variogram has known mathematical properties (such as positive definiteness) and is
used in kriging equations to determine the estimator weights. Possible valid models include expo-
nential, spherical, gaussian, linear, and power (Goovaerts, 1997).
The nugget effect (
z
) represents the random variability present in a data set at small distances.
By definition, the value of the variogram at a distance of zero is zero; however, data values can
display a discontinuity at very small distances. This apparent discontinuity at the origin could reflect
the unaccounted-for spatial variability at distances smaller than the sampling distance or could be
an artifact of the error associated with measurement.
The range (
C
0
A
) is the distance over which the samples are spatially correlated. The sill (
C
+
0
0
C
, variance attributed
purely to the process) and the nugget effect (Royle, 1980). It is the plateau that the model variogram
reaches at the range, and it is estimated by the sample variance only in the case of a model showing
a pure nugget effect. The model is fit to the empirical variogram visually and is optimized by
calculating the residual sum of squares (RSS). The values of the three main parameters are changed
iteratively to reduce the RSS value and fit the model.
) is the point of maximum variance and is the sum of the structural variance (
C
Sill (C + C
0
)
Structural Variance (C)
Nugget effect (C
0
)
Lag Distance (h)
Figure 14.1
Generic variogram including empirical data (circles) and model (heavy line).