Geoscience Reference
In-Depth Information
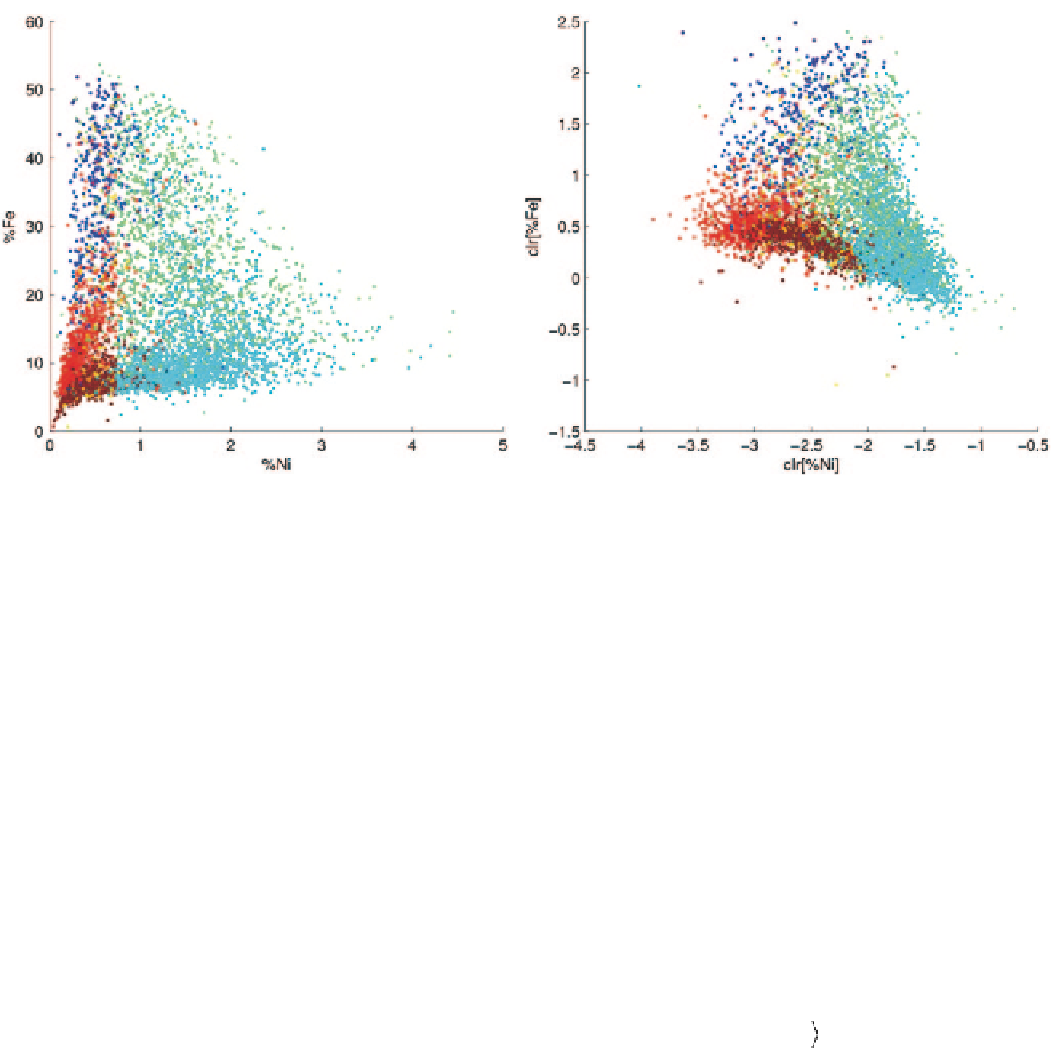
Fig. 5.15
Crossplots of Ni-Fe and clr(Ni)-clr(Fe)
Figure
5.15
shows the original and transformed scatterplots.
Compared to the alr transform, the data is now centered by
the geometric mean. This is better shown with a simplifica-
tion of the transformation on the Ni-Fe-SiO
2
subcomposition.
5.5.3.9 Isometric Logratio Transform
The isometric transform relies on orthonormal bases to trans-
form from the simplex to real coordinates and has the prop-
erty of conserving the metric properties in both spaces. Geo-
metric notions such as angles and distances in the simplex
are associated with angles and distances in the real space of
transformed data. Applying this transformation requires that
an orthonormal basis be defined in the Aitchison metric
(Egozcue et al.
2003
; Tolosana-Delgado et al.
2005
). The
Aitchison metric is the simplex sample space and geometry.
The orthonormal basis is defined by a set of vectors
e
1
,…,
e
d
and the interested reader is directed to Egozcue et al. (
2003
)
for a complete derivation. The ilr transform is defined given
these vectors, where
†
x
‡
(
)
y
=
log
i
=
log(
x
)
−
log
g
( )
x
ˆ
‰
i
i
Š
g
()
x
‹
5.5.3.8 Multiplicative Logratio Transform
This transformation is similar to the alr method except that
the divisor cannot be any one of the elements in the com-
position. Rather it is the filler required for a composition to
meet the unit sum constraint similarly to how
Z
was used
in the nickel laterite data. This transformation is appropri-
ate for exploring relationships between single divisions of
a composition (Aitchison
1986
). For example, analyzing
how the elements of Ni-Fe-SiO
2
relate to MgO-Co-Al
2
O
3
-
Cr
2
O
3
. The forward and inverse transformations are shown
below, with Fig.
5.16
showing graphically this transforma-
tion to the Ni-Fe-SiO
2
subcomposition.
⋅⋅
defines the Aitchison inner product.
,
a
y
=
xe
,
,
i
=
1,...,
d
i
i
a
D
∑
xx
,
=
clr(
x x
), clr(
)
=
clr(
x x
)
⋅
clr(
)
12
1
2
1
i
2
i
a
i
=
1
The Aitchison inner product is the Euclidean inner product (dot
product) applied to alr or clr transformed data. Transformation
using ilr calculates inner products of clr transformed data.
Despite the increased complexity of this transformation,
it has the advantage of generating vectors in unconstrained
orthogonal space (Fig.
5.17
). Any multivariate analysis tech-
nique can be applied to the result.
†
x
‡
y
=
log
i
,
i
=
1,...
d
ˆ
‰
i
Š
1
−−−
x
x
‹
1
i
exp(
y
)
x
=
i
,
i
=
1,...,
d
(
)
(
)
i
1
+ ⋅⋅+
exp(
y
)
1
exp(
y
)
1
i
1
x
=
+ ⋅⋅+
(
)
(
)
D
5.5.4
Service Variables
1
exp(
y
)
1
exp(
y
)
1
d
The use of accumulation (or service) variables in geosta-
tistics is fairly common in industry when developing block