Noise - Graphics Shaders - page 215

tic interpolation . Quintic interpolations are similar, but
they use a fifth-degree polynomial basis rather than
a cubic polynomial basis. The difference between the
two interpolations may be subtle; you will need to look
closely at the two value+gradient noise functions from
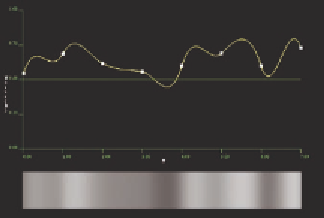
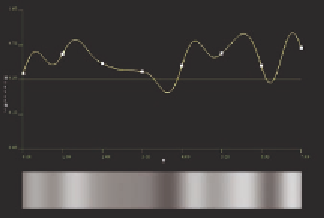
noisegraph in Figure 10.2 to see any difference. Cubic
interpolations are C 1 continuous (the curve has con-
tinuous slope), while quintic interpolations are C 2 con-
tinuous (the curve has both continuous slope and con-
tinuous curvature) and thus are smoother. One way to
think of the difference is that quintic functions main-
tain the curvature continuity at each connection point
by enlarging the overshoot there, not unlike racing past
second base in baseball. See [35] for a more complete
discussion.

Noise Equations
The key to understanding the derivation of the noise
functions is realizing that they are polynomial func-
tions whose coefficients are determined by the noise
properties you are using. Let's begin with cubic noise
functions and then go on to quintic functions.
Any cubic function of a single variable is given by a general cubic expres-
sion as

Figure 10.2. Cubic (top) and quintic
(botom) value+gradient interpolations
on the same basis.

() =+++

2 3 .

Nt ABtCt t

This expression gives the value, or position, of the function for any para-
metric value t . Because this expression has four unknowns, we need four
known quantities to determine them.
Now if we take the derivative of this expression, we get the gradient

dN
dt B t t

==+23 2

Gt () .

If we consider the values of the function and gradient at the endpoints of
the interval [0,1] in the parameter t ,

( ) == ( )

NNt == 0 N Nt 1

0 1

( ) == ( )

GGt == 0 G Gt 1

0 1