Hardware Reference
In-Depth Information
a
b
a
b
c
a
p
0
p
1
p
2
p
3
s
0
s
1
c
a
b
c
a
b
c
0
c
1
c
2
c
3
c
0
c
1
c
2
a
,
b
a
,
b
a
,
c
a
,
c
b
,
c
b
,
c
a
,
b
,
c
c
4
c
4
a
,
b
,
c
a
,
b
,
c
d
a
b
c
i
0
i
1
i
2
i
3
Fi
g. 15.4
Illustration of Example
15
.13
.(
a
)Plant
P
;(
b
) Specification
S
;(
c
) Largest solution
Pref
;(
d
) Composition
P
[
S
and largest controller
C
D
.P
[
S/
P
\
C
Proof.
If the equation is solvable then
S
P
,and
Pref
.S /
is a solution of the
equation.
Consider a string
˛
2
Pref
.S /
, then there exists a string
ˇ
such that
˛ˇ
2
S
,and
since
S
P
, it holds
˛ˇ
2
P
.Since
P
is deterministic,
˛ˇ
takes
P
to an accepting
state, i.e., each state of
P
\
Pref
.S /
is co-accessible.
t
Pref
However, it may be the case that for a solvable equation the solution
.P
[
S/
is
not progressive.
Example 15.13.
Consider a plant
P
Df
a; abc
g
and a s
pec
ification
S
Df
a
g
shown
Pref
respectively in Fig.
15.4
a,b. The largest solution
C
D
.P
[
S/
contains all the
words that do not start by
and it is shown in Fig.
15.4
c (represented by a non-
trim automaton because the state
abc
c
3
does not reach a final state). However
C
is not
progressive, because
P
\
C
is not trim, as seen in Fig.
15.4
d.
In supervisory control the notion of progressive supervisor plays the role of the
one of (compositionally) progressive solution of an equation over automata [38].
A solvable equation has the largest progressive supervisor that is obtained in the
same way as the largest (compositionally) progressiv
e s
olution of an equation over
automata, i.e., by deleting “bad” words from
Pref
, where a word is
C
D
.P
[
S/
“bad” if it is in
Pref
.P
\
C/
, but has no extension in
P
\
C
, i.e., it ends at a state
of
P
\
C
that is not co-accessible.
Example 15.14 (continues from
Ex
ample
15.13
).
By applying the trimming pro-
cedure to th
e
largest solution
Pref
.P
[
S/
we get the largest progressive solu-
Pref
tion
cProg
..P
[
S/
/
shown in Fig.
15.5
c. Examples of non-progressive and




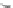

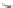

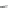
























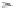





















Search WWH ::

Custom Search