Information Technology Reference
In-Depth Information
A.
B.
3
BP
HB
3
BP
2
HB
4
2
HB
2
HB
1
LP
TR
1
1
2.8
3
3.2
3.4
2.86
2.88
2.9
a
1
a
1
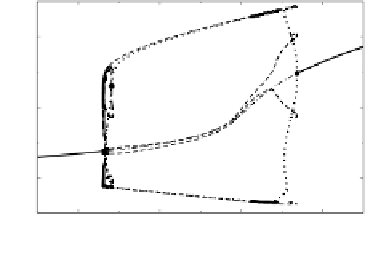
Fig. 3.11. A, bifurcation diagram obtained by variation in
1
. Other parameters:
2
= 5,
3
= 1,
4
= 4, = = = 2, d = 0:001, d
e
= 1 and = 0:01. B, detailed view of the region where
stable asymmetric solution exists. Between LP and T R, one oscillator has a large amplitude and
the other oscillates with small amplitude.
The Hopf bifurcations labeled HB
1
and HB
2
in Fig. 3.10 give rise to a branch of
periodic orbits, corresponding to a synchronous in-phase solution (see Fig. 3.9A).
The stability of this region is determined with two saddle-node bifurcations LP
1
and
LP
2
. It is important to note that the in-phase oscillations present in the system are
stable for all values of d, in contrast with the case of coupled repressilators discussed
above.
For small coupling (d < 0:01) anti-phase oscillations arise (Fig. 3.9B,C). The
periodic branch giving rise to the anti-phase solution is limited again by two Hopf
bifurcations: HB
2
at
1
= 2:869, and HB
3
at
1
= 3:336. However, their sta-
bility region is signicantly smaller than the corresponding stability region in the
repressilator model discussed in Sec. 3.2.2.
Another mode of collective behavior is the asymmetric regime, characterized by
the presence of large and small amplitude oscillations (see Fig. 3.9D,E). Although
this solution resembles the IHLC shown in 3.2.2, its bifurcation structure here is
completely dierent and very complex. In particular, for
1
= 2:882 a pitchfork
bifurcation (labeled BP in Fig. 3.11A,B) is found on the bifurcation branch that
gives rise to the anti-phase oscillations. Starting from this bifurcation point, a sec-
ondary bifurcation branch with a complex structure is observed (Fig. 3.11A). The
stable asymmetric solution lies within this branch; the stability region is depicted
with thick lines in Fig. 3.11B (zoomed region where a stable asymmetric solution
exists), the unstable asymmetric solution is shown with the dashed line. The asym-
metric regime is stabilized through a torus bifurcation at
1
= 2:877 (labeled as
T R in Fig. 3.11B). This bifurcation leads to two incommensurate frequencies. For
isolated oscillators (d = 0) and for
1
>
HB
1
, the rst frequency is that of a large
cycle, and the second one is determined by the eigenvalues of the unstable focus.
Slight diversity in the ensemble of relaxators does not alter the behavior shown
above (results not shown) and conrms the relevance of these ndings for biological
networks.