Information Technology Reference
In-Depth Information
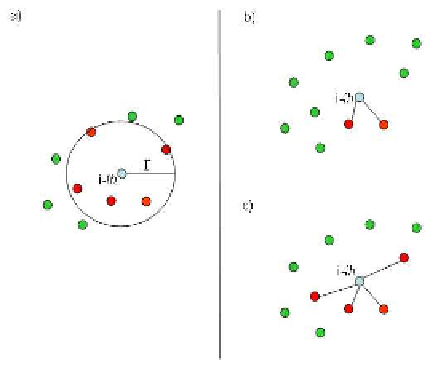
Fig. 17.10. Examples of r-disk neighboourhood (a), topological neighbourhood with two (b) and
four (c) neighbours.
which the interaction network is built by two dierent techniques: the r-disk and
the topological graph. In this last case, only the nearest N
n
agents are considered
neighbors and consequently part of the interaction network. In Fig. 17.10 an exam-
ple of r-disk neighborhood (a), topological neighborhood with two (b) and four (c)
neighbors, respectively, is illustrated.
To compare the two models, at rst the order parameter v
a
is evaluated with
respect to the agent density in the r-disk case, and to the number of neighbors N
n
in the topological case, for dierent values of the noise parameter . The parameter
N
n
seems to be a reasonable counterpart of in the topological case, since an
increase of both parameters leads in both cases to the inclusion of more agents in
the computation of the average heading. In Fig. 17.11 a similar behavior can be
observed for both r-disk (Fig. 17.11(a)) and topological (Fig. 17.11(b)) cases: v
a
tends to increase for increasing values of and N
n
, and to decrease for increasing
values of the noise parameter . The choice of the range for in the r-disk case is
made to achieve an average number of neighbors in the r-disk case (r
2
) equal to
the xed number of neighbors N
n
in the topological case (i.e., = N
n
=r
2
). With
this in mind, it can be observed from Fig. 17.11 that the topological graph performs
slightly better.
An interesting feature which distinguishes the behavior of the two models is the
reaction of the group to an attack by a predator. In [Ballerini et al. (2008)] the
authors claim that, although both ways of dening the interaction network provide
cohesion for suitable values of the parameters, topological interactions lead to a
more robust cohesion. This is shown by simulating the attack of a predator (the
approach of which causes a repulsive reaction in the other agents) in both models,
and evaluating the probability that the group does not break up or, on the opposite,
breaks into two or more connected components. Ballerini et al. (2008) conclude that