Evolutionary Models for Simple Biosystems - Biological Networks - page 359

2.0

G c

1.0

0.0 0.2 0.4 0.6 0.8

r

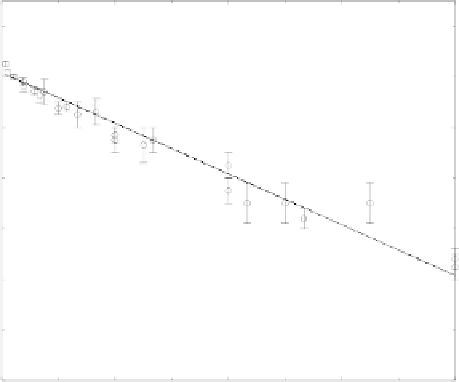
Fig. 15.11. Three-species coexistence boundary G c for = 2. The continuous line represents the
analytical approximation, Eq. (15.28), the circles are obtained from numerical simulations. The
error bars represent the maximum error (see text for details).

for less steep potentials, such as power law decrease, the coexistence condition is
supposed not to be fullled.
For = 2 the coexistence condition is given by
z 2 (G + r)z + 1 = 0 ;

z 2
2

Gz exp = 1 :

One can solve numerically this system and obtain the boundary G c (r) for the co-
existence. In the limit r!0 (almost at static tness) one has
G c (r)'G c (0)r (15.28)

with G c (0) = 2:216 : : : . Thus for G > G c (r) we have coexistence of three or more
quasi-species, while for G < G c (r) only the ttest one survives.
We have solved numerically Eq. (15.17) for several dierent values of the param-
eter G. We have considered a discrete phenotypic space, with N points, and a simple
Euler algorithm. The results, presented in Fig. 15.11, are not strongly aected by
the integration step. The error bars are due to the discreteness of the changing
parameter G. The boundary of the multi-species phase is well approximated by
Eq. (15.28); in particular, we have checked that this boundary does not depend
on the mutation rate , at least for < 0:1, which can be considered a very high
mutation rate for real organisms. The most important eect of is the broadening
of quasi-species curves, which can eventually merge as described in Section 15.3.4.1.
This approximate theory to derive the condition of coexistence of multiple quasi-
species still holds for the hyper-cubic genotypic space. The dierent structure of