Evolutionary Models for Simple Biosystems - Biological Networks - page 335

0011

0001 0111

0101

0010 1011

0000 1001 0110 1111

0100 1101

1010

1000 1110

1100

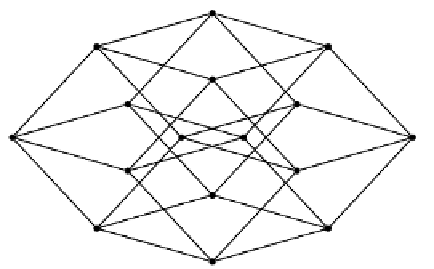
Fig. 15.1. The two-dimensional projection of the Boolean hypercube for L = 4.

Any base can assume one of four values (ATCG in DNA, AUCG in RNA). A
sequence of L basis can therefore assume one out of 4 L values. The space of all
possible sequences is called the sequence space. It is a high-dimensional, discrete
space.
Due to the extremely large number of possible sequences, there has not been
enough time during evolution to \try" all possible sequences nor a relevant fraction
of it. Therefore, we cannot apply \equilibrium" concepts to evolution.
The sequence space is well dened for a xed length L, but the length of the
genome in real organisms is not xed. In order to allow for variable L, one can
consider an extended space with an extra symbol \*", which stands for an empty
space, that can occasionally be replaced by a real basis. This is the same represen-
tation used to align sequences, to be illustrated in the following. We can assume
that between any subsequent couple of basis there are empty symbols.
For simple modeling, we limit our investigation to xed-length genomes g =
(g 1 ; : : : ; g L ), and assume that each component g i is a Boolean quantity, taking values
0 and 1. The quantity g i should represent \genes" in a rather general meaning.
Sometimes, we use g i to represent two allelic form of a gene, say g i = 0 for the
wild type, and g i = 1 for the less dangerous mutation, even if the quantity is not
a \gene" in the standard assumption (e.g., information to produce a protein). In
other contexts, g i might represent the presence or the absence of a certain gene, so
that we can theoretically identify of all possible genomes with dierent sequences.
Every possible sequence of length L corresponds to a corner in the Boolean,
L-dimensional hypercube (see Fig. 15.1). Each link in the hypercube correspond to
the change of one element g i , i.e., to a single-element mutation. Other mutations
correspond to larger jumps.
In the following, we shall denote by d(x; y) the genetic distance, i.e., the min-
imum number of mutations needed to pass from x to y. The quantity d(x; y) is a
topological concept, in real life one has to consider the probability of mutations in
order to estimate if a longer path could occur with higher probability. In our digital
approach, d(x; y) is just the Hamming distance between the two sequences.