Information Technology Reference
In-Depth Information
10000
1000
j
100
10
1
1
10
100
1000
10000
1e+05
N
coalesced
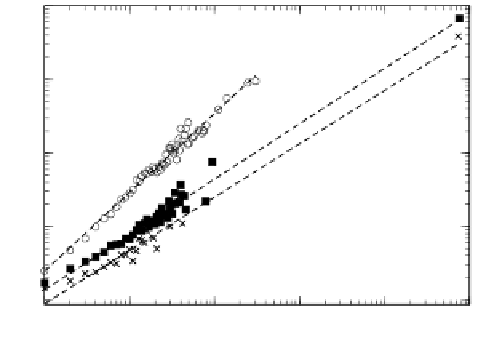
Fig. 6.3. Average degree of the nodes of the renormalized graph at T = 0:08 versus their size, mea-
sured in number of nodes of the un{renormalized graph that coalesced in each of them (N
coalesced
).
Data have been binned along the horizontal axis with step 1. Stars refer to the fast{folding het-
eropolymer, lled squares to the slow-folding heteropolymer and empty circles to the hydrophobic
homopolymer. Dashed lines are power law ts of exponents 0:73, 0:75 and 1:1.
As previously anticipated, the connectivity of the lowest energy node of the graph
deserves a separate consideration. First, it is important to stress that, following
renormalization, this becomes by far the most connected node in the graph. This
eect is denitely more pronounced in the case of the heteropolymers as one can see
in Fig. 6.3 where the lowest energy nodes correspond to the points on the extreme
right of the curves there displayed. We can conclude that, as far as connectivity
is concerned, the lowest energy node behaves somehow opposite to the rest of the
connectivity graph upon renormalization: it tends to acquire connections while the
rest of the graph tends to lose it. The eect is strong for the heteropolymers and
much weaker for the homopolymer.
One of the most informative topological quantity when studying diusion over
a graph is the spectral dimension of the graph itself. It has long been known that
recurrence and rst passage times in Markov chains on regular lattices diverge
with the system size for lattice dimensions higher than 2. These results have been
recently extended to general graphs by making use of the spectral dimension [20]
that is the exponent describing how the spectral density of the graph vanishes at low
eigenvalues. More specically the spectral density of the discrete Laplacian matrix
L
discrete
of an innite graph vanishes for low eigenvalues as !
d1
where d is dened
as the spectral dimension. This quantity still controls the rate of divergence of rst
passage times but loses many relations to other topological quantities: for example,
the dimensionality of a regular lattice is proportional to its average connectivity,
the spectral dimension of an irregular graph is not.
Although d is rigorously dened only for innite graphs, a closely related quan-
tity, d, can be computed also for nite graphs by means of an asymptotic power{law