Graphics Reference
In-Depth Information
Gabor wavelets are used to extract the appearance changes as a set of multi-
scale and multi-orientation coefficients. In our implementation, we use two
spatial frequency scales with wavelength of 5 and 8 pixels, and 6 orientations
at each scale. Thus for each point, we have 2
×
6 = 12 Gabor wavelets
coefficients. We choose to compute the Gabor wavelets coefficients of the
logarithm of denoted by Based on equation (7.1) and the
linearity property of Gabor transform, we have
where function
G
denotes a Gabor transform as in [Tian et al., 2002, Zhang
et al., 1998]. We impose a positive lower bound on pixel values in texture
and
I
to avoid singular situations. In our approach, only the magnitudes of
Gabor transform results are used because the phases are very sensitive to noise
in positions. Then we note that if it means the neutral face texture
I
contains more high frequency components than the deformed face texture
It could be caused by any of the following reasons: (1) the misalignment of
and
I
; (2) high gradient of log(
I
) due to low intensities of
I
; (3) flattening
of wrinkles and creases on neutral face during motion. Scenarios (1) and (2)
should be considered as noise, and (3) rarely happens in common human facial
motions. Thus we discard negative values of
In practice, we need to account for the foreshortening effect of the texture
projection. For a 3D face surface patch, the larger its visible area in input
image, the higher confidence we should have on the extracted features of the
corresponding texture patch. To this end, we construct a confidence map
following [Cascia et al., 2000], which is based on the ratio of each 3D surface
patch's projected area in the texture plane and its area in the input image. For
each facial motion region we compute a confidencecoefficient
as the average of the in this region. The resulting confidence coefficients
are used to weight the features in tracking described in Section 1.3.
contains noise due to misalignment of and
I
. To reduce the
influences of noise on the appearance feature, we construct another weight map
which tries to give large weight for features in deformed area and small
weight for features in un-deformed area. We define
in similar spirit as [Liu et al., 2001a], where is the normalized cross-
correlation coefficient between two patches centered at from
and
G
(log(
I
)). The idea is that high frequency components of and
log(
I
) should be close for un-deformed area, since and
I
are roughly aligned
by geometric-feature-based tracking. We use to compute the weighted
average of Gabor wavelets coefficients in the 11 selected regions. For each
region, an appearance feature vector of 12-dimension is computed.
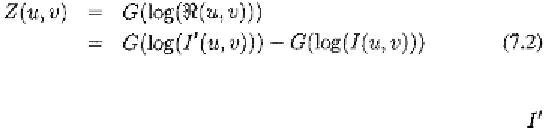

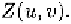

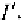

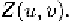



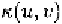


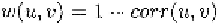
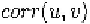
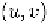

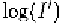
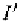

Search WWH ::

Custom Search