Graphics Reference
In-Depth Information
Using the notation of [Ramamoorthi and Hanrahan‚ 2001a]‚ the irradiance
can be represented as a linear combination of spherical harmonic basis func-
tions:
Ramamoorthi and Hanrahan [Ramamoorthi and Hanrahan‚ 2001a] showed that
for diffuse reflectance‚ only 9 coefficients are needed to approximate the irra-
diance function. Therefore‚ given an image of a diffuse surface with constant
albedo
its reflected radiance at a point with normal can be approximated
as
If we treat as a single variable for each and we can solve for these
9 variables using a least square procedure‚ thus obtaining the full radiance
environment map. This approximation gives a very compact representation of
the radiance environment map‚ using only 9 coefficients per color channel.
An important extension is the type of surface whose albedo‚ though not
constant‚ does not have low-frequency components (except the constant com-
ponent). To justify this‚ we define a function
such that
equals to the
average albedo of surface points whose normal is
We expand
using
spherical harmonics as:
where is the constant component and contains other higher order
components. Together with equation (6.6)‚ we have
If does not have first four order components‚ the second
term of the righthand side in equation (6.7) contains components with orders
equal to or higher than 3 (see Appendix A for the explanation). Therefore‚ if we
define
SpharmonicProj(I)
to the be function which projects the face image
I
into the 9 dimensional spherical harmonic space‚ we have
Therefore‚ the 9 coefficients of order
estimated from
with a lin-
ear least square procedure are
where
Hence‚




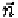






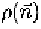








Search WWH ::

Custom Search