Graphics Reference
In-Depth Information
weight of each control point such that the trajectory has higher likelihood.
Intuitively, it can be achieved in a way that states with small variance pull the
trajectory towards them, while states with larger variance allow the trajectory to
stay way from them. Therefore we set the weights to be where
is the trajectory normal vector that also passes is the variance
of the Gaussian distribution in direction. In practice, it is not trivial to
compute Thus, we approximate it by normal vector of line segment
(see in Figure 5.1(a)). Compared to [Brand, 1999], the smooth
trajectory obtained is less optimal in terms of maximum likelihood. But it is
fast and robust, especially when the number of states is small or the assumed
HMM topology fits the data poorly. Ezzat et al. [Ezzat et al., 2002] propose an
trajectory synthesis approach similar in spirit to ours. But our formulation is
easier in a sense that it can viewed as a natural extension of traditional key-frame-
based spline interpolation scheme, given the probability distribution of each key
frame. Figure 5.1 shows a synthetic example comparing conventional NURBS
and our statistically weighted NURBS. The dots are samples of facial shapes.
Figure 5.1.
(a): Conventional NURBS interpolation. (b): Statistically weighted NURBS in-
terpolation.
The dashed line connects centers of the states. The solid line is the generated
facial deformation trajectory. In Figure 5.1(b), the trajectory is pulled towards
the states with smaller variance, thus have higher likelihood than trajectory
in Figure 5.1(a). Ezzat et al. [Ezzat et al., 2002] observed that the generated
trajectory by spline-based method could be “under-articulated”. To reduce
the undesirable effect, they proposed to adjust the center and variance of the
Gaussian model based on training data. We plan to perform similar adjustments
in our framework.
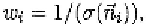
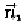
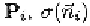
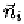

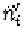


Search WWH ::

Custom Search