Graphics Reference
In-Depth Information
Figure 3.2.
The markers of the Microsoft data [Guenter et al., 1998]. (a): The markers are
shown as small white dots. (b) and (c): The mesh is shown in two different viewpoints.
3. Learning Holistic Linear Subspace
To make complex facial deformation tractable in computational models, peo-
ple have usually assumed that any facial deformation can be approximated by
a linear combination of some basic deformation. In our framework, we make
the same assumption, and try to find optimal bases under this assumption. We
call these bases
Motion Units
(MUs). Using MUs, a facial shape
can be
represented by
where
denotes the facial shape without deformation,
is the mean facial
deformation,
is the MU set, and
is the MU
parameter (MUP) set.
In this topic, we experiment on both of the two databases described in Sec-
tion 2. Principal Component Analysis (PCA) [Jolliffe, 1986] is applied to learn-
ing MUs from the database. The mean facial deformation and the first seven
eigenvectors of PCA results are selected as the MUs. The MUs correspond
to the largest seven eigenvalues that capture 93.2% of the facial deformation
variance, The first four MUs are visualized by an animated face model in Fig-
ure 3.3. The top row images are the frontal views of the faces, and the bottom
row images are side views. The first face is the neutral face, corresponding
to The remaining faces are deformed by the first four MUs scaled by a
constant (from left to right). The method for visualizing MUs is described in
Section 5. Any arbitrary facial deformation can be approximated by a linear
combination of the MUs, weighted by MUPs. MUs are used in robust 3D facial
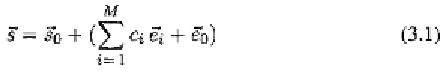
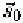
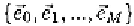
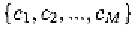
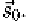
Search WWH ::

Custom Search