Geography Reference
In-Depth Information
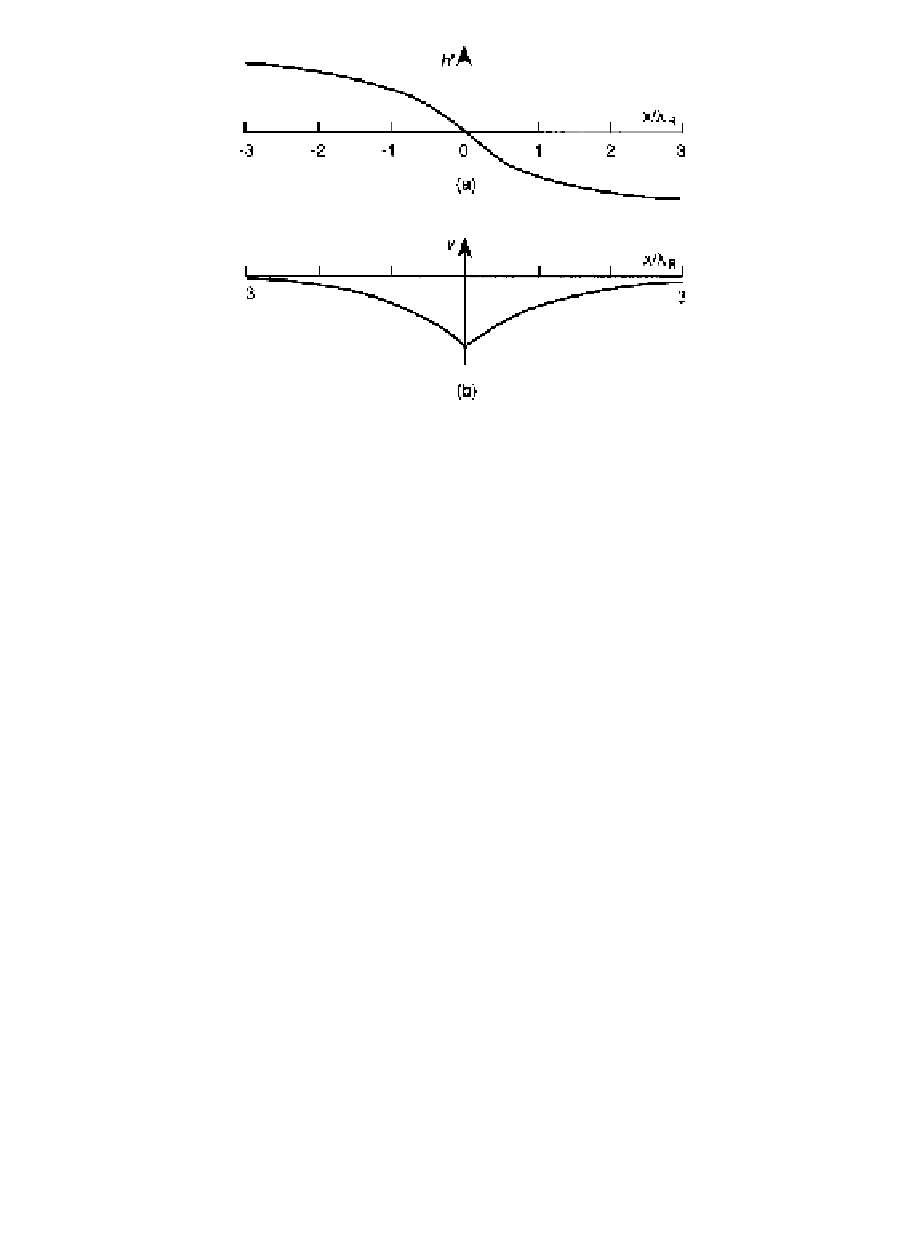
Fig. 7.13
The geostrophic equilibrium solution corresponding to adjustment from the initial state
defined in (7.78). (a) Final surface elevation profiles; (b) the geostrophic velocity profile in
the final state. (After Gill, 1982.)
0in
(7.69)-(7.71). That would yield geostrophic balance, and
any
distribution of h
would satisfy the equations:
Note that the result (7.84) could not be derived merely by setting ∂/∂t
=
g
∂h
g
∂h
∂u
∂x
+
∂v
∂y
=
f
0
u
=−
∂y
,
0
v
=
∂x
,
0
Only by combining (7.69)-(7.71) to obtain the potential vorticity equation, and
requiring the flow to satisfy potential vorticity conservation at all intermediate
times, can the degeneracy of the geostrophic final state be eliminated. In other
words, although any height field can satisfy the steady-state versions of (7.69)-
(7.71), there is only one field that is consistent with a given initial state; this field
can be found readily because it can be computed from the distribution of potential
vorticity, which is conserved.
Although the final state can be computed without solving the time-dependent
equation, if the evolution of the adjustment process is required, it is necessary to
solve (7.80) subject to the initial conditions (7.78), which is beyond the scope of
this discussion. We can, however, compute the amount of energy that is dispersed
by gravity waves during the adjustment process. This only requires computing the
energy change between initial and final states.
The potential energy per unit horizontal area is given by
h
ρgh
2
/2
ρgzdz
=
0