Circulation and Vorticity - An Introduction to Dynamic Meteorology - page 102

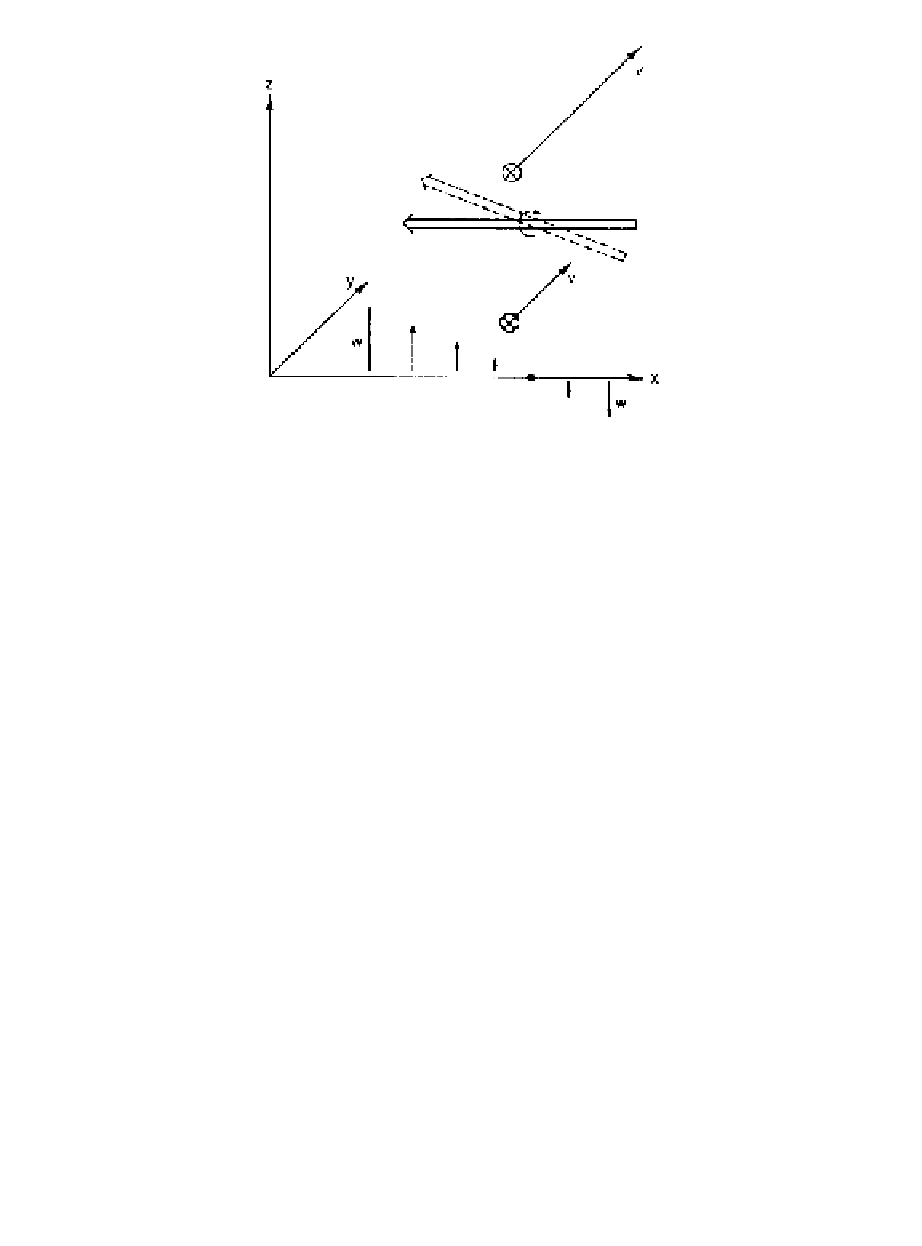
Fig. 4.12 Vorticity generation by the tilting of a horizontal vorticity vector (double arrow).

nonuniform vertical motion field. This mechanism is illustrated in Fig. 4.12, which
shows a region where the y component of velocity is increasing with height so
that there is a component of shear vorticity oriented in the negative x direction as
indicated by the double arrow. If at the same time there is a vertical motion field in
which w decreases with increasing x, advection by the vertical motion will tend
to tilt the vorticity vector initially oriented parallel to x so that it has a component
in the vertical. Thus, if ∂v/∂z > 0 and ∂w/∂x < 0, there will be a generation of
positive vertical vorticity.
Finally, the third term on the right in (4.17) is just the microscopic equivalent
of the solenoidal term in the circulation theorem (4.5). To show this equivalence,
we may apply Stokes' theorem to the solenoidal term to get

A ∇ ×

− αdp ≡− α ∇ p · d l =− (α ∇ p) · k dA

where A is the horizontal area bounded by the curve l . Applying the vector identity
∇ ×

(α ∇ p) ≡ ∇ α × ∇ p, the equation becomes

− αdp =− ( ∇ α × ∇ p) · k dA

A

However, the solenoidal term in the vorticity equation can be written

∂α
∂x

∂p
∂y −

∂α
∂y

∂p
∂x

− =− ( ∇ α × ∇ p) · k

Thus, the solenoidal term in the vorticity equation is just the limit of the solenoidal
term in the circulation theorem divided by the area when the area goes to zero.