The Challenge of Attaching Dissimilar Materials - Structural Interfaces and Attachments in Biology - page 13

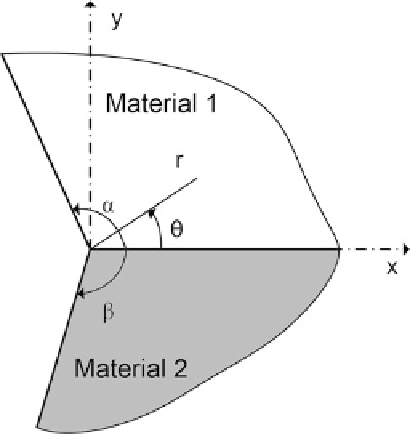
Fig. 1.9 Geometry in the
vicinity of the free edge at the
attachment between
two dissimilar materials
(the z -axis is perpendicular
to the plane)
effect of such a layer in dental and metal-to-bone interfaces and at the tendon-
to-bone insertion site has already been discussed. While the stiffness and stress
analyses could be conducted along the lines of previously cited studies, the
fracture problem is more challenging. One complication is related to several
possible scenarios of the crack propagation. For example, cracking can occur
along the bondline between the interfacial layer and one of the dissimilar
materials or alternatively, cracking can occur within the interfacial layer itself.
Finally, it is also possible for the crack to “depart” from the interfacial region
and propagate into one of the joined materials.
The orientation of the crack may be predicted adopting one of several available
criteria applicable to fracture in a functionally graded material. For example, such
criteria can include [ 21 ]:
- The maximum hoop stress criterion, i.e., the crack propagates along the axis of
the maximum hoop stress.
- The maximum strain energy release rate criterion, i.e., the crack propagates
along the axis corresponding to the maximum strain energy release rate.
- The maximum strain energy density criterion, i.e., crack propagation occurs with
the direction corresponding to the smallest strain energy density.
The previous discussion implies that an optimum interface is likely to be graded
in the direction perpendicular to the surfaces of joined dissimilar materials. The
case of a uniform interface can be treated as a particular case of the more general
graded counterpart. Numerous relevant problems have been considered in engi-
neering science (e.g., [ 22 - 24 ]), although the optimization of the interface arresting
the crack propagation has not been attempted.