Mechanics of Self-Similar Hierarchical Adhesive Structures Inspired by Gecko Feet - Structural Interfaces and Attachments in Biology - page 209

to the tangent of the surface. Motivated by this experiment, Gao et al. [ 7 ] performed
finite element calculations of the pull-off force of a single seta and, as shown in
their results plotted in Fig. 10.8b , confirmed theoretically that the pull-off force of
gecko's seta strongly varies with the pulling orientation, with the maximum value
achieved around

' ¼ 30 .
In the case of single contact by an elastic tape or seta, the anisotropic behavior of
the pull-off force can be attributed to the asymmetric alignment and slender
structure of the contacting object. While this behavior suggests that the pull-off
force of a single hair in contact can be controlled by pulling in different directions,
an open question is whether the adhesive strength of a large array of fibers or a
macroscopic attachment pad in contact with a rough surface would show similar
behaviors. To address this question, we shall consider the issue of releasable
adhesion from the point of view of continuum interfacial failure mechanics.
We use theoretical modeling and numerical simulations to show that strong elastic
anisotropy on the continuum level, achieved via fibrillar microstructures or some
other means, plays a key role in releasable adhesion: a strongly anisotropic elastic
solid also exhibits a strong orientational dependence of the pull-off force, similar to
the behavior of a single seta studied by Gao et al. [ 7 ].

10.4.3 Directional Adhesion Strength of an Anisotropic
Elastic Material

To illustrate the intrinsic orientation-dependence of adhesion strength of an aniso-
tropic elastic material in contact with a rough surface, we consider the linear elastic
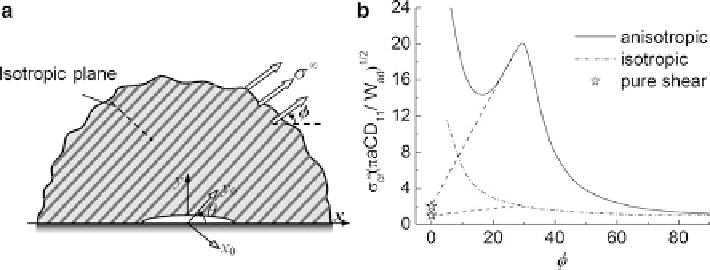
plane-strain problem shown in Fig. 10.9a where a transversely isotropic elastic half-
space ( y 0) is brought to contact with a rigid substrate. A plane-strain interfacial

Fig. 10.9 Releasable adhesion in three dimension. The pull-off stress of a strongly anisotropic
(transversely isotropic) elastic half-space sticking to a substrate. ( a ) An interfacial crack-like flaw
with width 2 a is introduced as a representative contact flaw due to surface roughness or
contaminants. ( b ) Variation of the adhesion stress as a function of the pulling angle for the
anisotropic material in comparison with that for an isotropic material