Biomedical Engineering Reference
In-Depth Information
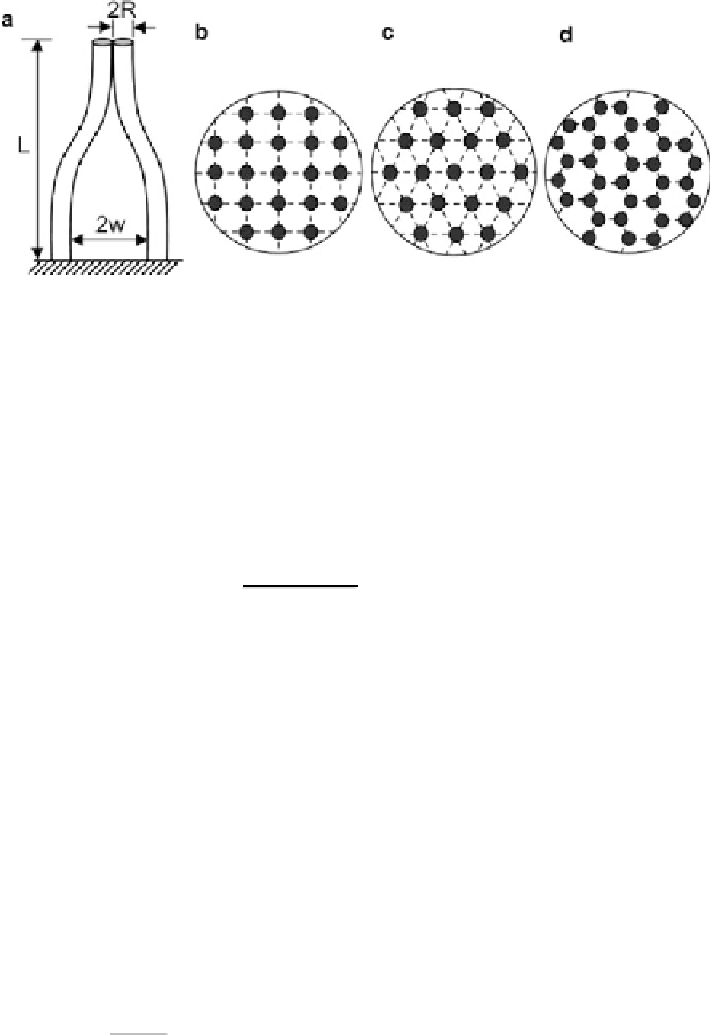
Fig. 10.4
Anti-bunching condition of a fibrillar structure. (
a
) Configuration of self-bunching in an
array of fibers distributed in (
b
)
square
,(
c
)
triangular
,or(
d
)
hexagonal
patterns
cause them to bundle together, as shown in Fig.
10.4a
. The stability condition can
be derived from the point of view of a maximum fiber length for spontaneous
separation of two fibers sticking together (e.g., [
7
]). In other words, given fiber
separation
w
and radius
R
, there exists a critical length
L
cr
beyond which lateral
bunching of neighboring fibers becomes stable configurations. Glassmaker et al.
[
33
] have derived the critical length for bunching of cylindrical fibers as
"
#
1
=
12
"
#
1
=
4
4
E
f
R
12
E
f
R
3
w
2
g
f
p
L
cr
¼
(10.5)
2
11
g
f
ð
1
n
2
f
Þ
Assuming that the fibers are distributed in a regular lattice pattern, one can relate
the fiber separation
w
, radius
R
to the area fraction
'
of a fiber array by
R ð
0
p
'
max
='
w ¼
1
<'<'
max
Þ
(10.6)
where
'
max
stands for the maximum area fraction of the given hair pattern. It can be
shown that
2
p
for a triangular lattice (Fig.
10.4b
),
'
max
¼ p=
'
max
¼ p=
4 for a
3
p
for a hexagonal lattice (Fig.
10.4d
). Inserting
square lattice (Fig.
10.4c
), and
p=
(
10.6
) into (
10.5
) leads to
1
=
3
1
=
2
p
'
max
='
E
f
R
g
f
L
cr
¼ Ra
1
(10.7)
1
=
12
3
3
4
p
where
a ¼
:
2
5
ð
1
n
2
f
Þ
Equation (
10.7
) has been derived for the lateral sticking between two neighboring
fibrils. Similar analysis can also be carried out for other possible bunching
configurations involving multiple neighboring fibers. We find that the critical fiber
Search WWH ::

Custom Search