Biomedical Engineering Reference
In-Depth Information
Fig. 8.7
The normalized
pull-off force as a function of
the normalized surface
undulation amplitude under
different values of the SCI
and wave numbers. Other
selected parameters are
g ¼
2,
l ¼
2.576, and
b ¼
1
0.7
α=0.1, 2πa/l=1
α=0.1, 2πa/l=2
α=0.1, 2πa/l=4
α=5, 2πa/l=1
α=5, 2πa/l=2
α=5, 2πa/l=4
0.6
0.5
0.4
0.3
0.2
1
0
0.2
0.4
0.6
0.8
h
0
/a
uniform at
a ¼
0.1 for different shapes. This analysis of specific adhesion via
receptor-ligand bond clusters demonstrates that optimal adhesion can be achieved
at any length scale by designing the shape of the contact surfaces. However, the
robustness of optimal adhesion against random shape variations can only be
achieved at sufficiently small contact size or for a small SCI,
a
.
In order to investigate the specific adhesion of a soft elastic body on a wavy
surface via a patch of molecular bonds, we consider a wavy surface profile,
hðxÞ
¼ h
0
½
1
þ
cos
ð
2
px=lÞ
. By solving (
8.15
) and (
8.17
) at steady state, Fig.
8.7
shows
the normalized pull-off force as a function of the amplitude of surface undulation
for different magnitudes of surface wavelength and SCI,
a
. It can be seen from
Fig.
8.7
that for relatively small adhesion size or SCI, the adhesion strength tends to
decrease monotonically as the surface amplitude increases. This can be understood
from the point of view that increasing surface amplitude leads to more non-uniform
stress distribution within the contact patch. For relatively large adhesion size or
SCI, there exists an optimal surface topography with a finite undulating amplitude
and an optimal wavelength on the same scale as the adhesion patch size for the
maximum adhesion strength.
8.5.5 Active Control of Focal Adhesions
Analysis of the SCI has shown that, depending on system parameters, there is a
transition between uniform stress (equal load sharing) and crack-like singular stress
distribution along the contact interface. It seems that an important parameter under
control by the cell is the stiffness of the cell body, as contractile forces can stiffen or
soften the actin network of the cytoskeleton, allowing the cell to modulate stress
distribution along the cell-substrate interface and, in so doing, control the stability
and growth/shrinkage of FAs.




































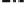

Search WWH ::

Custom Search