Biomedical Engineering Reference
In-Depth Information
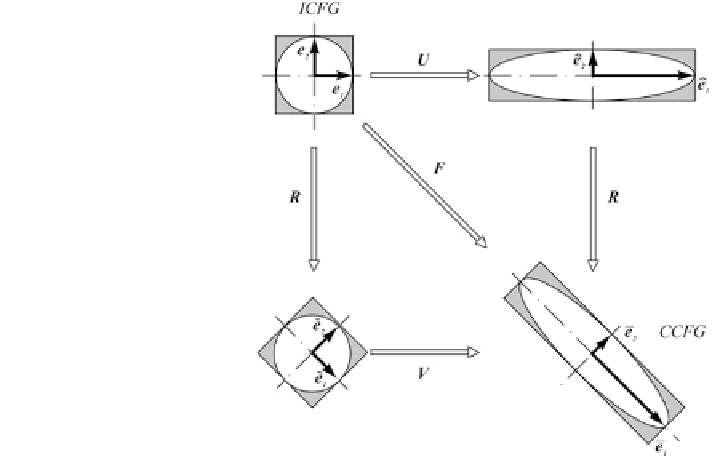
Fig. 3.14 Application of the
polar decomposition theorem
on a sphere
Polar Decomposition Theorem. According to (
3.49
), the deformation gradient
does not contain any translational parts but only rotational parts of the motion.
This can be seen as follows: two motions x
1
and x
2
¼
x
1
þ
c
ð
t
Þ
that differ only by
a (time-dependent) translation c
ð
t
Þ
have equal deformation gradients F
1
and F
2
since
due
to
spatial
independence
of
c
ð
t
Þ
the
term
c
ð
t
Þr
vanishes:
F
2
x
2
r¼½
x
1
þ
c
ð
t
Þr¼
x
1
rþ
c
ð
t
Þr¼
x
1
r
F
1
:
The rotational parts of the motion become apparent by polar decomposition
F
¼
R
U
¼
V
R
:
ð
3
:
59
Þ
where F may be decomposed uniquely into a right and a left stretch tensor U and
V, respectively, and a rotation tensor (or versor) R where U and V are symmetric
and positive definite tensors (x
6¼
0 is an arbitrary vector)
U
¼
U
T
;
V
¼
V
T
and
x
U
x [ 0
;
x
V
x [ 0
:
ð
3
:
60
Þ
Using U and V the configurational change of line-, area- and volume elements
etc. at unrotated principal directions may be described, i.e. only the extensions (or
compressions) of the particular object are described (cf. Fig.
3.14
). Tensor R is an
orthogonal tensor with
R
R
T
¼
R
T
R
¼
I
R
T
¼
R
1
and
with
det R
¼þ
1
:
ð
3
:
61
Þ
where R denotes a rigid body rotation of the principal directions (cf. Fig.
3.14
).
In general, tensor R changes at every continuum point and describes the rigid
rotation of a material line element (and the principal axis frame) but not the