Geology Reference
In-Depth Information
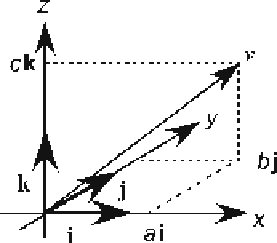
Fig. 12.2.
Vector components in the
xyz
coordinate system. Vector
components
i
,
j
,
k
each have
lengths equal to one
where the vertical bars = the absolute value of the expression between them. The di-
rection cosines of any vector can be normalized to generate a unit vector by dividing
each direction cosine (
l
,
m
, and
n
) by the right-hand side of Eq. 12.21.
12.4.1
Angle between Two Lines or Planes
The angle,
, between two lines, is given by the scalar or dot product of the two unit
vectors with the same orientations as the lines. If the two vectors represent the poles
to planes or the dip vectors of planes, then the dot product is the angle between the
planes, normal to their line of intersection (Fig. 12.3). The
dot product
is defined as
Θ
v
1
·
v
2
=|
v
1
| |
v
2
| cos
Θ
,
(12.22)
where |
v
| = 1 for a unit vector and
v
1
·
v
2
is evaluated as
v
1
·
v
2
=
l
1
l
2
+
m
1
m
2
+
n
1
n
2
,
(12.23)
where the subscript “1” = the direction cosines of the first vector and subscript “2” = the
direction cosines of the second vector. Equating 12.22 and 12.23 gives the angle be-
tween two unit vectors:
cos
Θ
=
l
1
l
2
+
m
1
m
2
+
n
1
n
2
.
(12.24)
12.4.2
Line Perpendicular to Two Vectors
The orientation of a line perpendicular to two other vectors is given by the vector prod-
uct, also called the cross product (Fig. 12.3). The
cross product
of two vectors is defined as
v
1
×
v
2
=
n
|
v
1
| |
v
2
| sin
Θ
,
(12.25)
where
n
= a unit vector perpendicular to the plane of
v
1
and
v
2
. When the vectors are
unit vectors given in terms of the direction cosines, the cross product is: