Binary search trees - Data Structures and Problem Solving Using Java - page 707

19.4.1 properties

Figure 19.21 shows two binary search trees. The tree shown in Figure 19.21(a)
satisfies the AVL balance condition and is thus an AVL tree. The tree shown in
Figure 19.21(b), which results from inserting 1, using the usual algorithm, is
not an AVL tree because the darkened nodes have left subtrees whose heights
are 2 larger than their right subtrees. If 13 were inserted, using the usual
binary search tree insertion algorithm, node 16 would also be in violation.
The reason is that the left subtree would have height 1, while the right subtree
would have height -1.

Every node in an
AVL tree has sub-
trees whose
heights differ by at
most 1. An empty
subtree has height
-1.

The AVL balance condition implies that the tree has only logarithmic
depth. To prove this assertion we need to show that a tree of height H must
have at least C H nodes for some constant C > 1. In other words, the minimum
number of nodes in a tree is exponential in its height. Then the maximum
depth of an N -item tree is given by log C N . Theorem 19.3 shows that every
AVL tree of height H has many nodes.

The AVL tree has
height at most
roughly 44 percent
greater than the
minimum.

figure 19.21
Two binary search
trees: (a) an AVL tree;
(b) not an AVL tree
(unbalanced nodes
are darkened)

12 12

8 16 8 16

4 10 14 4 10 14

2 6 2 6

1

(a) (b)

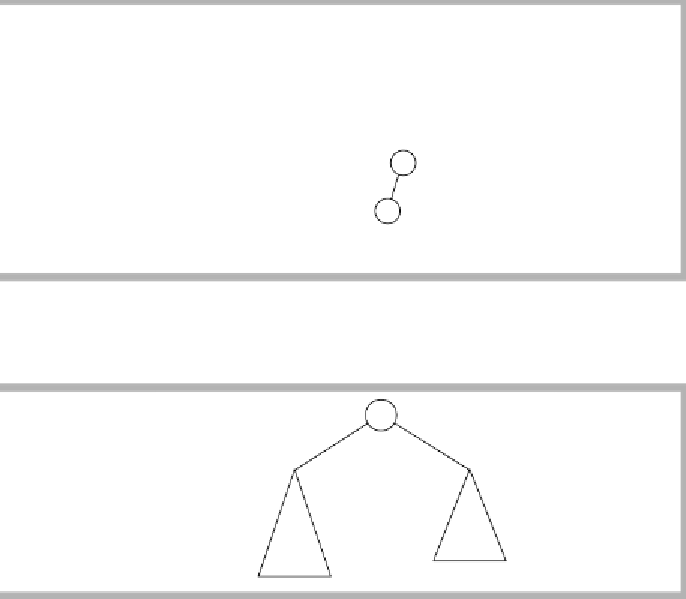
figure 19.22
Minimum tree of
height H

H

H - 2

H - 1

S H - 2

S H - 1