Binary search trees - Data Structures and Problem Solving Using Java - page 703

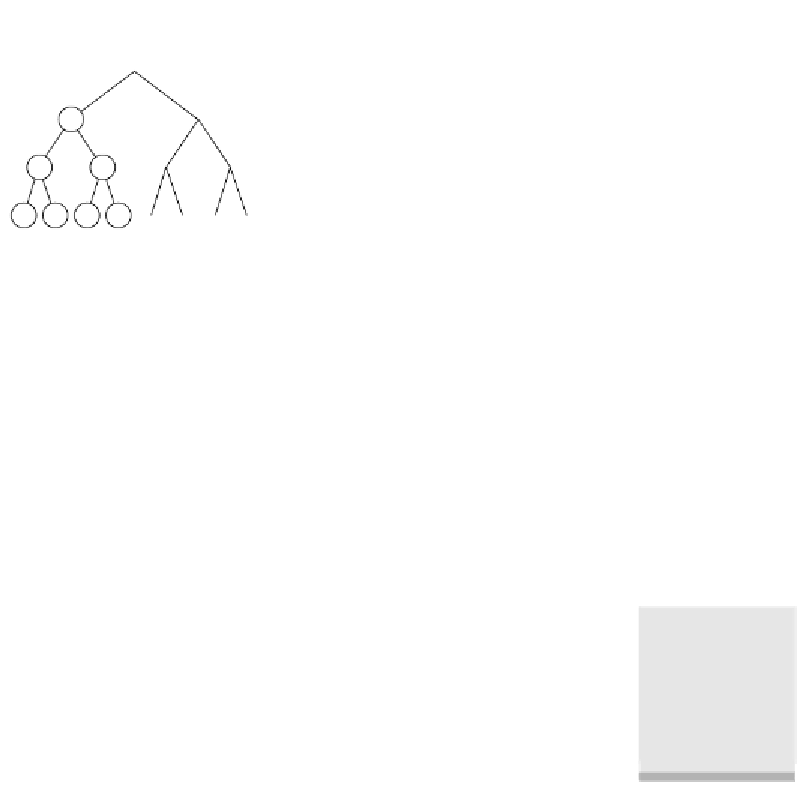
figure 19.19
(a) The balanced tree
has a depth of
⎣log N ⎦ ; (b) the
unbalanced tree has a
depth of N - 1 .

(a) (b)

Unfortunately, we have no guarantee that the tree is perfectly balanced. The
tree shown in Figure 19.19(b) is the classic example of an unbalanced tree. Here,
all N nodes are on the path to the deepest node, so the worst-case search time is
O ( N ). Because the search tree has degenerated to a linked list, the average time
required to search in this particular instance is half the cost of the worst case and
is also O ( N ). So we have two extremes: In the best case, we have logarithmic
access cost, and in the worst case we have linear access cost. What, then, is the
average? Do most binary search trees tend toward the balanced or unbalanced
case, or is there some middle ground, such as ? The answer is identical to that
for quicksort: The average is 38 percent worse than the best case.

N

We prove in this section that the average depth over all nodes in a binary
search tree is logarithmic, under the assumption that each tree is created as a
result of random insertion sequences (with no remove operations). To see
what that means, consider the result of inserting three items in an empty
binary search tree. Only their relative ordering is important, so we can
assume without loss of generality that the three items are 1, 2, and 3. Then
there are six possible insertion orders: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1),
(3, 1, 2), and (3, 2, 1). We assume in our proof that each insertion order is
equally likely. The binary search trees that can result from these insertions are
shown in Figure 19.20. Note that the tree with root 2, shown in
Figure 19.20(c), is formed from either the insertion sequence (2, 3, 1) or the
sequence (2, 1, 3). Thus some trees are more likely to result than others, and
as we show, balanced trees are more likely to occur than unbalanced trees
(although this result is not evident from the three-element case).
We begin with the following definition.

On average, the
depth is 38 percent
worse than the best
case. This result is
identical to that
obtained using
quicksort.

definition: The internal path length of a binary tree is the sum of the depths of its
nodes.