Java Reference
In-Depth Information
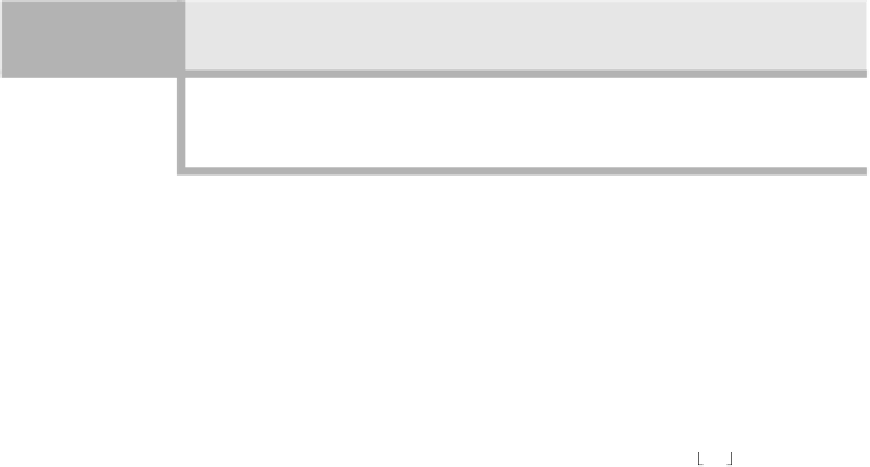
figure 9.8
Primality testing by
trial division
1
/**
2
* Returns true if odd integer n is prime.
3
*/
4
public static boolean isPrime( long n )
5
{
6
for( int i = 3; i * i <= n; i += 2 )
7
if( n % i == 0 )
8
return false; // not prime
9
10
return true; // prime
11
}
To do the primality test, we need an additional theorem, Theorem 9.2.
Theorem 9.2
If
P
is prime and
X
2
≡ 1(mod
P
)
, then
X
≡ ±1(mod
P
)
.
Proof
Because
X
2
- 1
0(mod
P
)
implies
(
X
- 1)(
X
+ 1)
0(mod
P
)
and
P
is prime, then
≡
≡
X
- 1
or
X
+ 1
0(mod
P
)
.
≡
A combination of Theorems 9.1 and 9.2 is useful. Let
A
be any integer
between 2 and
N
- 2. If we compute
A
N
- 1
(mod
N
) and the result is not 1, we
know that
N
cannot be prime; otherwise, we would contradict Fermat's Little
Theorem. As a result,
A
is a value that proves that
N
is not prime. We say then
that
A
is a
witness to N's compositeness.
Every composite number
N
has some
witnesses
A
,
but for some numbers, called the
Carmichael numbers
, these
witnesses are hard to find. We need to be sure that we have a high probability
of finding a witness no matter what the choice of
N
is. To improve our
chances, we use Theorem 9.1.
In the course of computing
,
we compute . So we let
and . Note that
X
and
Y
are computed automatically as
part of the
power
routine. If
Y
is 1 and if
X
is not ±1(mod
N
) , then by Theorem
9.1,
N
cannot be prime. We can return 0 for the value of when that condi-
tion is detected, and
N
will appear to have failed the test of primality implied
by Fermat's Little Theorem.
The routine
witness
, shown in Figure 9.9, computes
A
i
(mod
P
), aug-
mented to return 0 if a violation of Theorem 9.1 is detected. If
witness
does
not return 1, then
A
is a witness to the fact that
N
cannot be prime. Lines 12
through 14 make a recursive call and produce
X
. We then compute
A
i
(
A
)
i
⁄
2
2
XA
i
=
YX
2
=
⁄
2
A
i
X
2
, as is


Search WWH ::

Custom Search