Recursion - Data Structures and Problem Solving Using Java - page 305

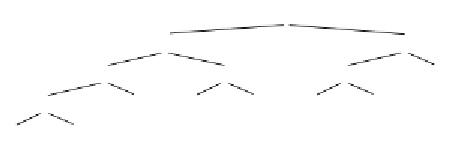
figure 7.7
A trace of the
recursive calculation
of the Fibonacci
numbers

F5

F4 F3

F3 F2 F2 F1

F2 F1 F1 F0 F1 F0

F1 F0

The underlying problem is that this recursive routine performs redundant
calculations. To compute fib(n) , we recursively compute fib(n-1) . When the
recursive call returns, we compute fib(n-2) by using another recursive call.
But we have already computed fib(n-2) in the process of computing fib(n-1) ,
so the call to fib(n-2) is a wasted, redundant calculation. In effect, we make
two calls to fib(n-2) instead of only one.
Normally, making two method calls instead of one would only double
the running time of a program. However, here it is worse than that: Each call to
fib(n-1) and each call to fib(n-2) makes a call to fib(n-3) ; thus there are actu-
ally three calls to fib(n-3) . In fact, it keeps getting worse: Each call to fib(n-2) or
fib(n-3) results in a call to fib(n-4) , so there are five calls to fib(n-4) . Thus we
get a compounding effect: Each recursive call does more and more redundant
work.

Let C ( N ) be the number of calls to fib made during the evaluation of fib(n) .
Clearly C (0) = C (1) = 1 call. For N

The recursive
routine fib is
exponential.

2, we call fib(n) , plus all the calls needed to
evaluate fib(n-1) and fib(n-2) recursively and independently. Thus
. By induction, we can easily verify that for

≥

CN () = CN 1 ( - ) + CN 2 ( - ) + 1

N 3 the solution to this recurrence is C ( N ) = F N + 2 + F N - 1 - 1. Thus the number

of recursive calls is larger than the Fibonacci number we are trying to compute,
and it is exponential. For N = 40, F 40 = 102,334,155, and the total number of
recursive calls is more than 300,000,000. No wonder the program takes forever.
The explosive growth of the number of recursive calls is illustrated in Figure 7.7.

≥

This example illustrates the fourth and final basic rule of recursion. The fourth funda-

mental rule of
recursion: Never
duplicate work by
solving the same
instance of a prob-
lem in separate
recursive calls.

4. Compound interest rule: Never duplicate work by solving the same

instance of a problem in separate recursive calls.

7.3.5 preview of trees

The tree is a fundamental structure in computer science. Almost all operating
systems store files in trees or tree-like structures. Trees are also used in com-
piler design, text processing, and searching algorithms. We discuss trees in
detail in Chapters 18 and 19. We also make use of trees in Sections 11.2.4
(expression trees) and 12.1 (Huffman codes).
One definition of the tree is recursive: Either a tree is empty or it consists
of a root and zero or more nonempty subtrees T 1 T 2 , , … , T k , each of whose