Algorithm analysis - Data Structures and Problem Solving Using Java - page 199

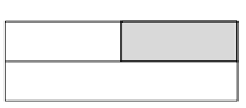
figure 5.6
The subsequences
used in Theorem 5.2

i j j + 1 q

S j + 1 , q

< 0

< S j + 1 , q

by not including it. This observation by itself is not sufficient to reduce the
running time below quadratic. A similar observation also holds: All contigu-
ous subsequences that border the maximum contiguous subsequence must
have negative (or 0) sums (otherwise, we would include them). This observa-
tion also does not reduce the running time to below quadratic. However, a
third observation, illustrated in Figure 5.7, does, and we formalize it with
Theorem 5.3.

For any i , let be the first sequence, with . Then, for any and
, either is not a maximum contiguous subsequence or is equal to an
already seen maximum contiguous subsequence.

A ij S ij < 0 i ≤≤ pj

Theorem 5.3

, ,

pq ≤ A pq

,

Proof

If pi = , then Theorem 5.2 applies. Otherwise, as in Theorem 5.2, we have

. Since j is the lowest index for which S iq = S ip 1 + S pq S ij < 0 , it follows that

, , - , ,

S ip 1 ≥ 0 . Thus S pq ≤ S iq . If qj > (shown on the left-hand side in Figure 5.7), then

, - , ,

Theorem 5.2 implies that A iq is not a maximum contiguous subsequence, so neither

,

is A pq . Otherwise, as shown on the right-hand side in Figure 5.7, the subsequence

has a sum equal to, at most, that of the already seen subsequence

,
A pq A iq .

, ,

figure 5.7
The subsequences
used in Theorem 5.3.
The sequence from p
to q has a sum that is,
at most, that of the
subsequence from i to
q . On the left-hand
side, the sequence
from i to q is itself not
the maximum (by
Theorem 5.2). On the
right-hand side, the
sequence from i to q
has already been
seen.

i j j + 1 q i q j

S i, q S i, q

<= S i, q <= S i, q

>=0

>=0

p - 1 p

p - 1 p