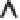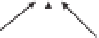Geoscience Reference
In-Depth Information
Time steps
(a)
x
t
+1
t
t
t
-1
x
i
-1
i
i
+1
Space increments
Time steps
(b)
x
t
+1
t
t
t
-1
x
i
-1
i
i
+1
Space increments
Figure B5.3.2
Schematic diagram of (a) explicit and (b) implicit time stepping strategies in approximate
numerical solutions of a partial differential equation, here in one spatial dimension, x (arrows indicate the
nodal values contributing to the solution for node (i,t
1
); nodal values in black are known at time t;
nodal values in grey indicate dependencies in the solution for time t
+
1
).
When an equation involves both space and time differentials, the simplest (but not neces-
sarily the most accurate) solution is to evaluate all the spatial differentials at time step
j
and use
them to solve for the dependent variable at time step
j
+
1. In this strategy, the calculations for
each node can be carried out independently of all the other nodal values at time
j
+
1 as shown
in Figure B5.3.2a. This is known as a solution that is
explicit
in time. It results in a solution
algorithm that has many attractions in that it is not necessary to assemble large matrices and
the solution is easily implemented on parallel computers. The disadvantage is that the solution
is only conditionally stable, especially for problems that are strongly nonlinear, such as those
encountered in hydrology. Thus, it is necessary to ensure that the time step is short enough
that the solution remains stable. For nonlinear problems, this may mean that very small time
steps are required. It is possible to calculate a stability criterion and to ensure that the time step
is small enough to ensure stability. The smaller the spatial discretisation used, in general, the
smaller the time step that is required to ensure stability. Such criteria take the form
t
+
cx
,
where
c
is a local wave speed and
x
is the local space increment of the model discretisation.
=