Graphics Reference
In-Depth Information
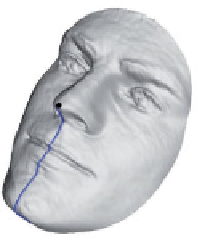
Nose tip
Upper lip
Lower lip
(a) Face with open
mouth
(c) Face with closed
mouth
(b) Best reparametrization
before matching
Figure 3.7
An example of matching of two radial curves extracted from two faces. (a) A curve on an
open mouth, (c) a curve on closed mouth, (b) change of parametrization before matching. Copyright
C
1969, IEEE
curves so that points reached at the same time on two curves are as close as possible under
some geometric criterion. In other words, peaks and valleys should be reached at the same
time. Figure 3.6
b
illustrates the matching, where point 1 on the top curve matches point 11 on
the down curve. The part between the point 1 and 2 on the top curve shrinks on the curve 2.
Therefore, the point 2 matches the point 12 on the second curve. An elastic metric is the
measure of that shrinking.
The use of SRV representation allows the reparametrization group to act by isometry on the
manifold of SRV representations. This point is very important as the curve matching could
be done after reparametrization. The change of parametrization before the matching is able to
reduce the effect of stretching and/or stretching of the curve.
This idea is illustrated in Figure 3.7. The task is to match two radial curves on two faces
with two different expressions. The expression in the face at the left induces open mouth in
contrast with the expression in face at the right. As shown in the middle panel, the anatomic
points on the curves (upper and down lips) match together after reparametrizing one curve.
More formally, the elastic matching of the curves allows better matching of anatomical points
on them.
3.5.2 Geometry of Preshape Space
We denote
3
2
(
I
3
) as the space of all unit-length, elastics
C
={
q
:
I
→ R
,
q
=
1
}⊂L
,
R
curve. The space
is in fact an infinite-dimensional unit-sphere and represents the preshape
space of all open elastic curves invariant to translation and uniform-scaling.
With the
C
2
L
metric on its tangent spaces,
C
becomes a Riemannian manifold. In particular,
3
).
To compare the shapes of two radial curves, we can compute the distance between them in
2
norm,
2
(
I
since the elements of
C
have a unit
L
C
is a hypersphere in the Hilbert space
L
,
R
C
under the chosen metric. This distance is defined as the length of a geodesic connecting the