Geology Reference
In-Depth Information
surface
a
X
2
sin
a
cos
a
(r
0
,0,0)
strike - slip
X
1
fault
plane
(r,
q
,
f
)
q
X
3
centre of mass
sin2
a
cos2
a
dip - slip
f
Figure 9.6 Fault geometry and focal force systems.
point is
r
=
(
x
1
,
x
2
,
x
3
), while the radius vector to a point on the fault surface is
r
=
(
x
1
,
x
2
,
x
3
) with the fault dip at an angleα to the horizontal. Volterra's formula
for a dip-slip fault gives the displacement vector at the field point as
u
⎣
⎝
⎠
∂
u
i
(
r
,
r
)
∂
u
i
(
r
,
r
)
∂
x
3
u
i
(
r
)
=
S
μ
Δ
∂
x
2
−
sin 2α
⎝
⎠
⎦
∂
u
i
(
r
,
r
)
∂
x
2
∂
u
i
(
r
,
r
)
∂
x
3
+
dS
,
−
cos 2α
(9.60)
with the slip,
Δ
u
3
=Δ
u
sinα. Volterra's
formula for a strike-slip fault gives the displacement vector at
Δ
u
, having components
Δ
u
2
=Δ
u
cosαand
the field
point as
S
μ
Δ
u
1
⎣
⎝
⎠
∂
u
i
(
r
,
r
)
∂
u
i
(
r
,
r
)
∂
x
1
u
i
(
r
)
=
∂
x
2
+
sinα
⎝
⎠
⎦
∂
u
i
(
r
,
r
)
∂
u
i
(
r
,
r
)
∂
x
1
dS
,
−
∂
x
3
+
cosα
(9.61)
with the slip having the single component
u
1
. These forms of Volterra's formula
allow the displacement field to be interpreted as being due to the superposition of
the displacement fields of a continuous distribution of dipole forces over the fault
surface. We take the systems of dipole force distributions shown in Figure 9.6 to
be located at
r
0
with spherical polar co-ordinates (
r
0
,θ
0
,0) on the fault surface.
The unit forces entering Volterra's formula are products of unit vectors with the
scalar densities
Δ
δ(
r
−
r
0
)δ(θ
−
θ
0
)δ(φ)
r
2
sinθ
δ
=
,
(9.62)








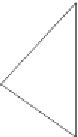























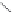
















Search WWH ::

Custom Search