Graphics Reference
In-Depth Information
(a)
(b)
00
10
20
30
00
01
10
11
(e)
010
011
00
01
11
21
31
02
03
12
13
012
013
1
02
12
23
32
20
21
30
31
02
03
03
13
22
33
22
23
32
33
(c)
(d)
300
301
31
302
303
2
320
321
33
322
323
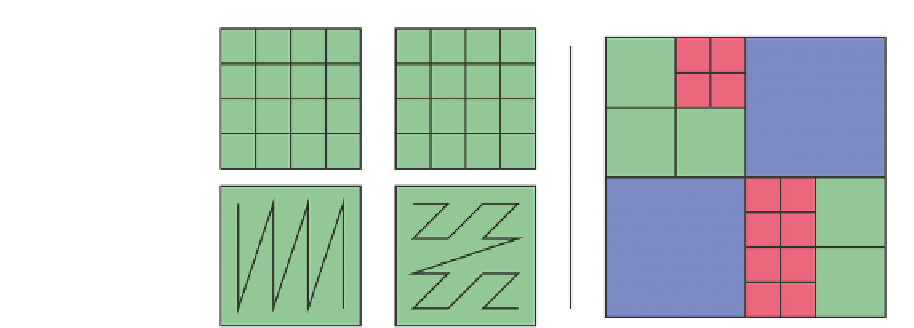
Figure 3.1.
(a) Column major ordering versus (b) Morton ordering and (c,d) the curves
they form. The curve formed by Morton ordering in (d) is often denoted as a Z-order
curve. (e) Bit codes of a linear quadtree, built from the ordering of (b). The subdivision
levels for the blue, green, and red nodes are respectively 1, 2, and 3.
in the next section. At render time, a square subdivision patch is instanced with
a unique location and scale for each node. By employing a distance-based LOD
criterion, we will show that T-junctions can be removed completely using a simple
tessellation shader.
3.2 Linear Quadtrees
Linear quadtrees were introduced by Gargantini as a nonrecursive alternative to
regular quadtrees [Gargantini 82]. In this data structure, each node is represented
by its subdivision level and a unique bit code, and only the leaves are stored in
memory. The code is a concatenation of 2-bit words, each identifying the quadrant
in which the node is located relative to its parent. If these words are chosen
so as to form a Z-order curve, then their concatenation forms a Morton code.
In Figure 3.1, for instance, the codes 0, 1, 2, and 3 are mapped to the upper
left (UL), upper right (UR), lower left (LL), and lower right (LR) quadrants,
respectively. This last property allows direct translation to row/column major
numbering (Figure 3.1(e)) by bit de-interleaving the code.
3.2.1 Representation
Similarly to Shaffer [Shaffer 90], we use a single integer to represent each node.
The rightmost bits are reserved for the subdivision level, and the adjacent bits are
left for the bit code. Below is the bit representation of the 32-bit word encoding
the red node whose code is 321 in Figure 3.1. Bits irrelevant to the code are
denoted by the “
_
” character.