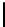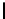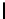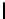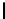Graphics Reference
In-Depth Information
•
NN:
A
is non-transposed,
B
is non-transposed:
N−
1
C
[
i,j
]=
α
A
[
i,k
]
×
B
[
k,j
]+
βC
[
i,j
]
.
k
=0
•
NT:
A
is non-transposed,
B
is transposed:
N−
1
C
[
i,j
]=
α
A
[
i,k
]
× B
[
j, k
]+
βC
[
i,j
]
,
k
=0
where
i
=0
,...,N
1.
CPU implementations of the NN variant often first transpose
B
and then
perform the NT variant, which has a more cache-friendly memory access pattern,
as we show in Section 7.5.4.
−
1and
j
=0
,...,N
−
7.5.3 Scalar Implementations
We first consider scalar implementations with an
N
N
ND-range covering all el-
ements of
C
. From our experience with optimizing the Sobel filter, these versions
are clearly suboptimal as they do not use any vector operations. We will (due to
their simplicity) use them to introduce our notation for describing memory access
patterns of kernels, and we will also use them as examples in some qualitative
discussions later.
×
Non-transposed.
Each work-item of the
scalarNN
version in Listing 7.9 produces
one element of
C
by computing the dot product of a row of
A
and a column of
B
.
kernel void
sgemm
(
global float const
A
,
global float const
B
,
global float
C
,
float
alpha
,
float
beta
,
uint
n
)
{
uint
j
=
get global id
(0);
uint
i
=
get global id
(1);
float
ABij
=0.0
f
;
for
(
uint
k
=0;
k
<
n
;++
k
)
{
ABij
+=
A
[
i
n
+
k
]
B
[
k
n
+
j
];
C
[
i
n
+
j
]=
alpha
ABij
+
beta
C
[
i
n
+
j
];
}
Listing 7.9.
Initial scalar implementation:
scalarNN
.