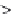Geoscience Reference
In-Depth Information
Fig. 8.9 Isometric view of a small
anticlastic water-air
interface element (heavy
lines), with a surface area
r
1
δθ
1
r
2
δθ
2
. After a small
virtual displacement
δ
r
(with
δθ
1
and
δθ
2
held
constant), the element
has an area (
r
1
+
δ
r
)
δθ
1
(
r
2
− δ
r
)
δθ
2
.
r
1
δθ
1
δ
r
r
2
δθ
2
are on the same side of the interface; it is called
anticlastic
when they are on opposite
sides. Equation 8.3 is commonly attributed to Laplace and can be derived as follows.
Derivation of the Laplace equation
Because the surface tension
represents the energy required to maintain the interface, it is
convenient to make use of the principle of virtual work. Thus consider a small anticlastic
surface element (
σ
(
r
1
δθ
1
r
2
δθ
2
) as shown in Figure 8.9. Let this element now undergo
a virtual displacement
δ
r
, such that the angles
δθ
1
and
δθ
2
are constrained to remain the
same infinitesimal fraction of
π
, but the radii of curvature become (
r
1
+
δ
r
) and (
r
2
−
δ
r
).
As a result of this displacement the area of the element becomes [(
r
1
+
δ
r
)
δθ
1
(
r
2
−
δ
r
)
δθ
2
].
With these preliminaries, the work required to perform this displacement can be equated
with the energy required to maintain the change in surface area of the element, as
follows
δ
x
δ
y
)
=
−
p
(
r
1
δθ
1
r
2
δθ
2
)
δ
r
=
σδθ
1
δθ
2
[(
r
1
+
δ
r
)(
r
2
−
δ
r
)
−
r
1
r
2
]
(8.4)
After canceling the superfluous terms, and after neglecting the remaining term in
δ
r
,
Equation (8.3) results immediately. A similar derivation can be constructed for a synclastic
interface.