Geoscience Reference
In-Depth Information
α
y
1
c
0
t=
0
0.2
0.4
0.8
1.2
0.5
0
−
2
−
1
0
1
2
x
m
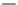
Fig. 5.7 Illustration of the motion of a disturbance, whose initial distribution is given by
Equation (5.55). This disturbance is made up of two components, which are one half of the
original disturbance and which are moving away in opposite directions from the origin
x
m
=
0.
The origin itself is moving downstream with a velocity
V
0
. The curves are obtained with
Equation (5.56) for
c
0
t
m
=
0, 0.2, 0.4, 0.8, and 1.2.
Example 5.5. Semi-infinite channel with known upstream inflow
A situation which has been the subject of many studies is that of a channel reach, with a
given inflow at its upstream end. If the upstream end is taken as the origin, where
x
=
0,
the boundary and initial conditions can be written as
y
(0
,
t
)
=
y
u
(
t
);
x
=
0
,
t
>
0
y
(
∞
,
t
) finite;
x
→∞
,
t
>
0
y
(
x
,
0)
=
0;
x
>
0
,
t
=
0
∂
y
(
x
,
0)
∂
t
(5.59)
=
0;
x
>
0;
t
=
0
These conditions can now be used with Equation (5.49) to solve the problem. However,
rather than to attempt a frontal attack, it is convenient here to make use of the d'Alembert
solution (5.58) for the unit impulse derived in the previous example, and by inspection of
Figure 5.7. This shows immediately that the component of that solution moving to the left
away from
x
=
0 can be considered an image, and that the component moving into the
domain
x
>
0 is the desired result. Thus one has the unit response function, that is the
solution for an input
δ
(
t
)at
x
=
0,
u
=
u
(
x
,
t
)
=
δ
(
x
−
(
V
0
+
c
0
)
t
)
(5.60)
If the input at
x
=
0 is actually
y
=
y
u
(
t
) instead of a delta function, the solution can be
readily obtained by convolution. For instance, in the case where
y
(
t
) represents the flow