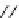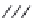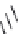Geoscience Reference
In-Depth Information
Fig. 5.4
An open channel with a
trapezoidal cross section. In
this case the cross-sectional
area is
h
(
B
s
+
B
b
)
/
2 and the
wetted perimeter is
P
w
=
[(
B
s
−
B
b
)
2
B
s
h
+
4
h
2
]
1
/
2
+
B
b
.
B
b
Empirical equations
Most empirical equations derived from uniform steady flow measurements are of the
form
C
r
R
h
S
f
V
=
(5.39)
where
C
r
is a resistance factor, which ideally depends only on the nature of the channel,
and
a
and
b
are constants;
R
h
is the hydraulic radius defined as
A
c
P
w
R
h
=
(5.40)
in which
A
c
is the cross-sectional area of the channel, and
P
w
the wetted perimeter of
that area. In two-dimensional flow situations and wide channels, the hydraulic radius
equals the depth of the flow, or
R
h
=
h
.
Example 5.2
This can be seen in the case of a channel with a trapezoidal cross section with a water
depth
h
, a bottom width
B
b
and a water surface width
B
s
(see Figure 5.4); according to
(5.40), this has a hydraulic radius
h
(
B
s
+
B
b
)
/
2
R
h
=
B
b
which approaches
h
as both
B
s
and
B
b
become large (compared to
h
) and practically
equal to each other.
[(
B
s
−
B
b
)
2
+
4
h
2
]
1
/
2
+
Probably the oldest form of open channel equation (5.39) is the one developed in
France by Chezy around 1770 in which
a
/
2
(Mouret, 1921). Numerous expres-
sions have been proposed for
C
r
(see Chow, 1959, p. 94, for a review). Some insight can
be gained in the nature of
C
r
, by comparing Chezy's equation with the more theoretically
based expressions for turbulent flow. It can be seen from the similarity expression for
wide channels (5.36), that in the Chezy equation the resistance factor
C
r
is given by
C
r
=(
g
=
b
=
1
k
)
1
/
2
[ln(
h
1]; this indicates that
C
r
depends not only on the roughness
but also on the hydraulic radius. It can also be seen from the power function expression
(5.38), that
C
r
is independent of
h
, and therefore of
R
h
, only if
m
/
/
z
0
)
−
=
0, that is when