Graphics Reference
In-Depth Information
B
C
A
D
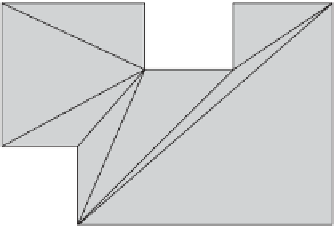
Figure 12.21
The Hertel-Mehlhorn algorithm turns a polygon triangulation into a convex
decomposition by deletion of as many diagonals as possible.
// The mesh is now a convex decomposition of the polygon. Return it
return m;
}
Instead of having a separate second pass in which diagonals are deleted, this
deletion can be incorporated into the actual triangulation process. As an ear is clipped,
it is tested against the previously cut polygon. If merging the cut triangle with the
previous polygon would form a convex polygon, the merge is performed. Otherwise,
the previously cut polygon is output, and the just cut ear is kept as the new “previous
polygon.”The test itself can be performed in constant time by testing the convexity
of the vertices where the triangle would attach to the previous polygon.
It can be shown that any convex partitioning that does not contain unnecessary
edges will have at most four times the minimum number of convex pieces. Typically,
for real-world cases the Hertel-Mehlhorn algorithm produces partitions not far from
optimal.
It is possible to change the triangulation algorithm slightly to generate even bet-
ter partitions, in general. The improvement consists of making the algorithm prefer
creating diagonals that connect to at least one concave vertex to those that connect
two convex vertices. For example, in Figure 12.21 replacing the diagonal between the
convex vertices
A
and
B
with one from
C
to
D
would result in a convex decomposition
into three instead of four pieces, which here is the optimum.
12.5.3
Convex Decomposition of Polyhedra
Just as intersection tests with convex polygons are faster than tests with arbitrary
polygons, intersection tests on polyhedra are much more efficient if the polyhedra are
convex. Nonconvex polyhedra are therefore best broken into convex pieces, allowing