Graphics Reference
In-Depth Information
n
2
P
2
A
Q
4
Q
3
Q
2
n
1
P
1
Q
1
B
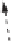
Figure 11.12
Intersecting segment
AB
against planes
P
1
and
P
2
(scale exaggerated).
11.6
Further Suggestions for Improving Robustness
In addition to the strategies covered in this chapter to this point, the following are
some suggestions for further improving the robustness of numerical calculations and
geometrical algorithms.
Test critical algorithms by implementing a reference algorithm, using a different
(perhaps brute-force) method. Run the two algorithms in parallel. If they do
not agree to some
k
significant digits, find out why.
●
Use defensive programming practices extensively. Add asserts to verify that
computed intersection points actually lie on the (thick) plane or that a
reflected velocity points away from the plane. However, beware (floating-point)
inaccuracies in the assert statement itself!
●
Make sure all possible special cases are covered by a routine. For example,
most triangle-triangle intersection tests require special code to handle the two
triangles lying in the same plane. Consider also how the triangle-triangle routine
handles one or both triangles degenerating to a line segment or to a point. Pay
special attention to how boundaries of objects are tested.
●
It is possible to test how susceptible a calculation is to accumulated and amplified
rounding errors by running the calculation in all rounding modes offered by the
(IEEE-754) floating-point arithmetic. If the output varies more than is expected,
the computation is unstable and should be reformulated.
●
Avoid using several different formulas for computing the same value.
Differences due to accumulated errors will introduce inconsistencies when the
computed values are used as decision variables. (Compare the sharing of the
scalar triple product, described in Section 11.3.3.)
●