Graphics Reference
In-Depth Information
e
B
r
L
C
P
= ?
D
A
(a)
(b)
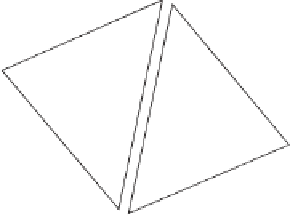
Figure 11.10
(a) As seen in Section 11.3.3, floating-point errors can have line
L
pass between
triangles
ABC
and
ADB
without intersecting either. (b) By testing using fat objects, such as a
capsule, even outright gaps in the geometry can be accommodated as long as the radius
r
of
the fat object is greater than
e
/2, where
e
is the width of the widest gap.
arithmetic, tolerance is built into the computations themselves by specifying each
value as a range
b
.
Special operators are defined in order to perform arithmetic on these interval values,
producing new interval values as results. Some common operators are defined as
follows:
[
a
,
b
]
of possible values, symbolizing some value
x
such that
a
≤
x
≤
[
a
,
b
]+[
c
,
d
]=[
a
+
c
,
b
+
d
]
[
a
,
b
]−[
c
,
d
]=[
a
−
d
,
b
−
c
]
[
a
,
b
]∗[
c
,
d
]=[
min(
ac
,
ad
,
bc
,
bd
), max(
ac
,
ad
,
bc
,
bd
)
]
]
[
[
a
,
b
c
,
d
]=[
a
,
b
]∗[
1/
d
,1/
c
]
for
0 /
∈[
c
,
d
]
0, max(
a
2
,
b
2
)
[
]
if 0
∈[
a
,
b
]
2
[
a
,
b
]
=
min(
a
2
,
b
2
), max(
a
2
,
b
2
)
[
]
otherwise
Unlike regular floating-point arithmetic, interval arithmetic provides bounds on
rounding errors, and an interval arithmetic computation essentially amounts to a
mathematical proof that the true value of an expression lies within the computed
bounds. These bounds can then be compared against those of other entities in order
to, for example, say with certainty that two objects are not intersecting if the bounds
are distinct.
The next section presents a few simple examples of interval arithmetic. The section
thereafter explores how interval arithmetic applies to collision detection problems.