Graphics Reference
In-Depth Information
p
0
P
P
p
1
s
0
q
1
r
0
q
0
Q
s
1
Q
s
1
(a)
(b)
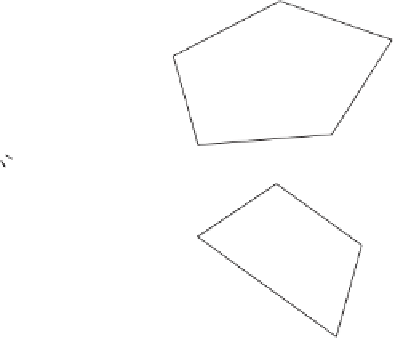
Figure 9.16
(a) The first iteration of the CW algorithm for polygons
P
and
Q
. (b) A separating
vector is found in the second iteration.
Figure 9.16 illustrates two steps of the main algorithm. In Figure 9.16a
s
0
is the initial
candidate vector for which the supporting vertices
p
0
and
q
0
are computed. These do
not indicate that
s
0
separates
P
and
Q
, and thus
s
0
is reflected in the perpendicular
r
0
to the (unit) vector
r
0
from
p
0
to
q
0
to give a new candidate vector
s
1
. In the
next iteration of the algorithm, illustrated in Figure 9.16b, the supporting vertices
p
1
and
q
1
now show that
s
1
is a separating vector and the algorithm terminates with
nonintersection for the two polyhedra.
A subalgorithm is used to terminate the CW algorithm when the polyhedra inter-
sect. It attempts to find a vector
m
such that
m
k
. If no such
vector can be found, the origin must lie inside the Minkowski difference of
P
and
Q
,
and the polyhedra intersect. The provided algorithm is
O
(
k
), where
k
is the number
of iterations performed. To reduce execution time, the subalgorithm can be executed
on every
n
-th iteration rather than on every iteration.
The motivation for the update rule used (in step 4) is that for two spheres it pro-
vides a separating vector in one step. A proof of convergence for this rule is given in
[Chung96]. It states that if
v
is any separating vector for
P
and
Q
then
s
k
+
1
·
r
i
≥
0 for 0
≤
i
≤
v
,
decreasing the angle between the candidate separating vector and the true separating
vector on each iteration and thus showing convergence. However, [Bergen99] notes
that the given proof is flawed and that it is only shown that
s
k
+
1
·
v
>
s
k
·
v
. Con-
vergence for the CW algorithm is thus not quite proven. Even so, the CW algorithm
appears to behave well in practice. By tracking the separating vector for two objects
and using it as the initial candidate vector of a subsequent test, the CW algorithm
runs in near constant time. In [Bergen99] the CW algorithm is reported twice as fast
(on average) as a separating-axis-enhanced version of GJK. Experiments reported in
·
v
≥
s
k
·