Graphics Reference
In-Depth Information
P
2
Y
P
P
3
p
p
2
p
3
P
1
p
1
Z
X
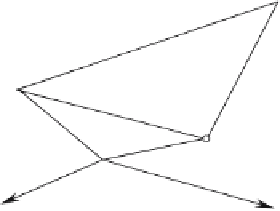
Figure 6.19.
Figure 6.19 shows a triangle P
1
P
2
P
3
with position vectors
p
1
p
2
, and
p
3
. Given a point P,
which resides on the plane containing P
1
P
2
, and P
3
, we can state that
p
=
r
p
1
+
s
p
2
+
t
p
3
(6.32)
where r
+
s
+
t
=
1 and 0
≤
rst
≤
1.
Eq. (6.32) can be written as
⎡
⎤
r
s
t
=
p
1
p
2
p
3
⎣
⎦
p
and is solved using Cramer's rule with
pp
2
p
3
p
1
p
2
p
3
p
1
pp
3
p
1
p
2
p
3
p
1
p
2
p
p
1
p
2
p
3
r
=
s
=
t
=
(6.33)
If r s, and t satisfy the above constraints, then
p
is inside the triangle, otherwise it is outside
the triangle's boundary. We will test these formulas in Section 6.15.
6.14 A sphere intersecting a plane
Detecting collisions between irregular objects is difficult. However, it is greatly simplified by
enclosing an object within a tight-fitting sphere and calculating collisions between spheres. As
part of this analysis, let's investigate the geometric relationship between a sphere and a plane.
But apart from finding the conditions for collision, let's also compute the curve of intersection
when a sphere intersects a plane.
We begin by positioning a sphere with radius R and centre C x
C
y
C
z
C
juxtaposed with a
plane defined by
ax
+
by
+
cz
=
d
where
n
ˆ
=
a
i
+
b
j
+
c
k