Graphics Reference
In-Depth Information
If we evaluate Eq. (4.10) using abc, and M, we obtain
−
x
−
y
−
z
=−
1
(4.11)
We can tidy up Eq. (4.11) by multiplying throughout by -1 to give
x
+
y
+
z
=
1
Now let's examine the ideas behind 3D space partitioning.
4.7 3D space partitioning
In Section 3.5 we discovered how it was possible to determine whether a point was inside or
outside a convex boundary. The technique also revealed whether a point was on a boundary
vertex or edge. Now let's explore a similar technique where we can determine whether a point
is inside, outside, or on a vertex, edge, or surface forming a convex polyhedron.
A simple example reveals the underlying mechanism of this form of 3D space partitioning.
A unit cube has been chosen aligned with the x-, y-, and z-axes, as it keeps the mathematics
very simple. However, it should be obvious from this example that the mathematical reasoning
holds for any convex polyhedron.
Y
Y
Y
P
v
v
u
n
v
n
n
P
u
X
X
X
P
u
Z
Z
Z
Y
Y
Y
u
P
v
v
P
n
n
u
n
X
X
X
u
v
P
Z
Z
Z
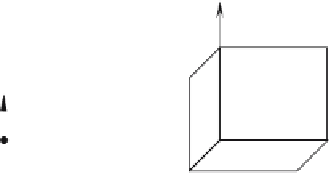
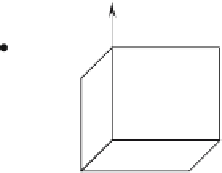
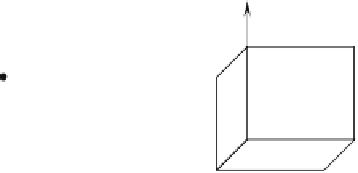
Figure 4.9.
Figure 4.9 shows six views of a unit cube with each surface highlighted with its normal vector
n
. To ensure that all the normal vectors point inwards, it is derived from two similar edges
forming each surface. We assume that the surfaces are defined by a chain of edges defined in a
counter-clockwise sequence when viewed from the outside, as shown in Fig. 4.9.