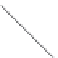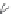Java Reference
In-Depth Information
f(5)
f(4)
f(3)
f(3)
f(2)
f(2) f(1)
f(2) f(1)
FIGURE 14.1:
Example of computing the fifth Fibonacci number recursively.
14.2 Dynamic Programming
The king liked the program and tried to run it on his brand-new supercomputer. To
his amazement, the program never gave him an answer. He waited and waited, but the
program never terminated. The king became worried. Had he failed to add a base case and
inadvertently made the program run forever? Careful consideration shows that this is not
the case. The problem is that the program is too slow and runs in exponential time. It
performs the same computations multiple times and is not feasible for larger input.
Having seen Figure 14.1, the king decided that a different approach was in order. How
can the program avoid making the same computations over and over again? The easiest
way is to save the result once it is computed. The program can save the result for
f(0)
,
f(1)
,
f(2)
, and so on. In other words, a bottom-up approach may be called for (instead of
the top-down approach of recursion). Here is the new program that the king wrote.
public class
Test
{
public static void
main(String args [])
{
long
sum = 0L ;
for
(
int
i=1;i
<
= 64; i++)
{
sum = sum + f ( i ) ;
System. out . println (sum) ;
}
public static long
f(
int
day)
{
if
(day == 1)
{
return
1L;
if
(day == 2)
{
return
1L;
long
a[] =
new long
[day + 1];
a[1] = 1L;
a[2] = 1L;
for
(
int
i=3;i
<
= day ;
i ++)
{
a[i] =a[i
−
1] + a[ i
−
2];
return
a[day];
}
}