Graphics Reference
In-Depth Information
and the areas of circumscribed polygons tend to the same limit, then
that common limit will be the area to be determined, provided the
boundary is continuous.
G
H
A
F
E
D
O
B
C
Figure10.2
1 (
Fermat
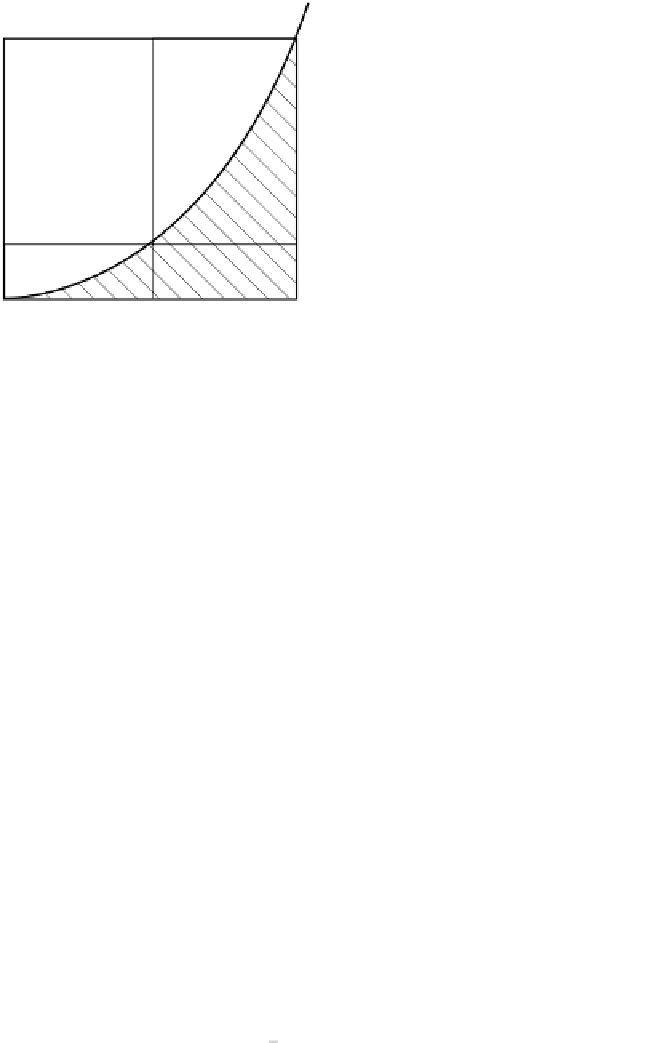
, 1636) We start by investigating the shaded area,
A
,
bounded by the parabola
y
x
, the
x
-axis and theline
x
a
,
taking
a
to bepositiv. In figure10.2
O
(0, 0),
B
(
a
, 0),
C
(
a
, 0),
D
(0,
a
),
E
(
a
,
a
),
F
(
a
,
a
),
G
(
a
,
a
) and
H
(
a
,
a
).
Justify the inequalities
area
BEFC
A
area
ODEB
area
BGHC
,
and deduce that
a
A
a
a
a
.
By inscribing rectangles with bases (
a
, 0)(
a
, 0) and (
a
,0)(
a
, 0), in
A
,
show that 5
a
/27
A
, and, by covering
A
with rectangles with
bases (0, 0)(
a
,0)(
a
, 0) show that
A
14
a
/27.
In thefirst case
A
was shown to liewithin an intrval of size
a
, 0), (
a
, 0)(
a
, 0) and (
a
,
and in thescond case
A
was shown to liewithin an intrval of size
a
, so thegap was narrowed.
Now, for a positive integer
n
, inscribe rectangles with bases
(
a
/
n
, 0)(2
a
/
n
, 0), (2
a
/
n
, 0)(3
a
/
n
, 0), . . ., ((
n
1)
a
/
n
, 0)(
a
, 0), in
A
, to show
that
a
n
(1
2
...
(
n
1)
)
A
.
Useqn 1.1 to show that
a
(1
1/
n
)(1
1/2
n
)
A
.