Individual Neurons - Computational Explorations in Cognitive Neuroscience - page 39

which provides a crude but very efficient approximation
to the neural dynamics of integrating over inputs. Thus,
we use equation 2.8 to compute a single membrane po-
tential value V m for each simulated neuron, where this
value reflects a balance of excitatory and inhibitory in-
puts. This membrane potential value then provides the
basis for computing an activation output value as dis-
cussed in a moment. First, we highlight some of the
important differences between this point neuron model
and the more abstract ANN approach.
Perhaps one of the most important differences from a
biological perspective is that the point neuron activation
function requires an explicit separation between excita-
tory and inhibitory inputs, as these enter into different
conductance terms in equation 2.8. In contrast, the ab-
stract ANN net input term just directly adds together in-
puts with positive and negative weights. These weights
also do not obey the biological constraint that all the in-
puts produced by a given sending neuron have the same
sign (i.e., either all excitatory or all inhibitory). Further-
more, the weights often change sign during learning.
In our model, we obey the biological constraints on
the separation of excitatory and inhibitory inputs by typ-
ically only directly simulating excitatory neurons (i.e.,
the pyramidal neurons of the cortex), while using an ef-
ficient approximation developed in the next chapter to
compute the inhibitory inputs that would be produced
by the cortical inhibitory interneurons (more on these
neuron types in the next chapter). The excitatory input
conductances ( g e (t) ) is essentially an average over all
the weighted inputs coming into the neuron (although
the actual computation is somewhat more complicated,
as described below), which is much like the ANN net
input computation, only it is automatically normalized
by the total number of such inputs:

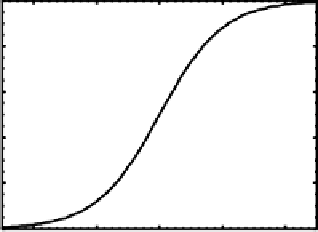
Box 2.1: Sigmoidal Activation Function

Sigmoidal Activation Function

1.0

0.8

0.6

0.4

0.2

0.0

−4 −2 0 2 4

Net Input

The sigmoidal activation function, pictured in the above
figure, is the standard function for abstract neural network
models. The net input is computed using a linear sum of
weighted activation terms:

where ￿ j is the net input for receiving unit j , x i is the acti-
vation value for sending unit i ,and w ij is the weight value
for that input into the receiving unit.
The sigmoidal function transforms this net input value into
an activation value ( y j ), which is then sent on to other units:

￿ ￿

input values approach a fixed upper limit of activation,
and likewise for the lower limit on strongly inhibitory
net inputs. Nonlinearity is important because this al-
lows sequences of neurons chained together to achieve
more complex computations than single stages of neu-
ral processing can — with a linear activation function,
anything that can be done with multiple stages could
actually be done in a single stage. Thus, as long as
our more biologically based activation function also ex-
hibits a similar kind of saturating nonlinearity, it should
be computationally effective.
To implement the neural activation function, we use
the point neuron approximation discussed previously,

(2.13)

Another important difference between the ANN ac-
tivation function and the point neuron model is that
whereas the ANN goes straight from the net input to the
activation output in one step (via the sigmoidal func-
tion), the point neuron model computes an intermedi-
ate integrated input term in the form of the membrane