Hebbian Model Learning - Computational Explorations in Cognitive Neuroscience - page 122

Note that this analysis adopts the simplification of mul-
tiplying C by the weight vector itself instead of its
expected value, assuming that it is changing relatively
slowly. Thus, the matrix C serves as the update func-
tion for a simple linear system over the state variables
represented by the weight vector w j . Itiswellknown
that this results in the state variables being dominated
by the strongest eigenvector (component) of the update
matrix.

∆ w

.1 .1 −.1 .4 .4 .4 .8 .8 −.8 2.4 2.4 2.4

y

j .1 −.4 −.8 2.4

w .1 .1 .1 .2 .2 0 .6 .6 .4 1.4 1.4 −.4

x

i

1 1 −1 −1 −1 −1 −1 −11 1 11

t=0 t=1 t=2 t=3

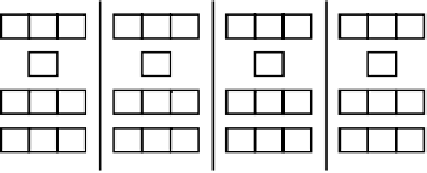
Figure 4.7: Demonstration of the simple Hebbian algorithm,
where the first two units are perfectly correlated with each
other, and the third is completely uncorrelated. For each input
pattern x i , y j is computed as

4.4.2 Oja's Normalized Hebbian PCA

, and then the change
in weights ￿w ij (which is added in at the next time step) is
computed as x i y j .

One problem with the simple Hebbian learning rule is
that the weights become infinitely large as learning con-
tinues. This is obviously not a good thing. Fortunately,
it is relatively simple to normalize the weight updat-
ing so that the weights remain bounded. Although we
will not end up using exactly this algorithm (but some-
thing rather similar), we will explain how a very influ-
ential version of Hebbian learning achieves this weight
normalization. This algorithm was proposed by Oja
(1982), who developed the following modified Hebbian
learning rule, which subtracts away a portion of the
weight value to keep it from growing infinitely large:

will increase because this average correlation value will
be relatively large. Interestingly, if we run this learn-
ing rule long enough, the weights will become domi-
nated by the strongest set of correlations present in the
input, with the gap between the strongest set and the
next strongest becoming increasingly large. Thus, this
simple Hebbian rule learns the first (strongest) principal
component of the input data.
A simple, concrete demonstration of this learning
rule is shown in figure 4.7, where there are 3 input units
and the single linear output unit. Over the 4 different in-
put patterns, the first two units are perfectly correlated
with each other, while the third is perfectly uncorrelated
(and all units have zero mean, as we assumed). No-
tice how the two correlated units “gang up” against the
uncorrelated one by determining the sign (and magni-
tude) of the hidden unit activation y j , which then en-
sures that their weights just keep increasing, while the
uncorrelated one's weights “thrash” up and down. If
you run through another iteration of these patterns, you
will notice that the weights for the two correlated ones
increase rapidly (indeed, exponentially), but the uncor-
related one remains small due to the thrashing.
For the more mathematically inclined, we can say
that the simple Hebbian learning rule adapts the weights
toward the principal eigenvector (i.e., the one with the
largest eigenvalue ) of the correlation matrix C . This can
be seen by rewriting equation 4.6 in vector notation:

(4.9)

￿ w = ￿ ( x ￿ y

To understand how this learning rule keeps the
weights from growing without bound, we can consider
the simple case where there is just one input pattern (so
we can avoid the need to average over multiple patterns)
and look for a stable value of the weight after learning
for a long time on this one pattern. We simply need to
set the above equation equal to zero, which will tell us
when the equilibrium or asymptotic weight values have
been reached (note that this is the same trick we used in
chapter 2 to find the equilibrium membrane potential):

(4.10)

Thus, the weight from a given input unit will end up
representing the proportion of that input's activation rel-
ative to the total weighted activation over all the other

(4.8)

￿ w = Cw