Hebbian Model Learning - Computational Explorations in Cognitive Neuroscience - page 121

Σ k

to read. Furthermore, we assume that each time step
corresponds to a different pattern of activity over the
inputs.
Let's assume that the weights into the receiving unit
learn on each time step (input pattern) t according to a
very simple Hebbian learning rule (formula for chang-
ing the weights) where the weight change for that pat-
tern ( ￿ t w ij , denoted dwt in the simulator) depends
associatively on the activities of both presynaptic and
postsynaptic units as follows:

y = x

k w kj j

Σ k

∆

<x x > < t

w ij = w kj

i

k t

w ij

<x x >

= C ik

i k t

. . .

x x

i k

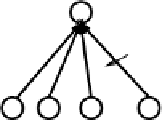
Figure 4.6: Schematic for how the correlations are computed
via the simple Hebbian learning algorithm.

which is just a linear function of the activities of all the
other input units, we find that, after a little bit of algebra,
the weight changes are a function of the correlations
between the input units:

(4.2)

where ￿ is the learning rate parameter ( lrate in the
simulator) and i is the index of a particular input unit.
The learning rate ￿ is an arbitrary constant that deter-
mines how rapidly the weights are updated as a function
of each experience — we will see in chapter 9 that this is
an important parameter for understanding the nature of
memory. The weight change expression in equation 4.2
(and all the others developed subsequently) is used to
update the weights using the following weight update
equation:

￿ w = h x

(4.6)

h w

This new variable C ik is an element of the correla-
tion matrix between the two input units i and k ,where
correlation is defined here as the expected value (av-
erage) of the product of their activity values over time
( C ik = hx i x k i t ). You might be familiar with the more
standard correlation measure:

(4.3)

( t +1)= w ( t )+￿

t

To understand the overall effect of the weight change
rule in equation 4.2, we want to know what is going to
happen to the weights as a result of learning over all
of the input patterns. This is easily expressed as just
the sum of equation 4.2 over time (where again time t
indexes the different input patterns):

(4.7)

h( x ￿ ￿ )( x ￿ ￿

which subtracts away the mean values ( ￿ )ofthevari-
ables before taking their product, and normalizes the
result by their variances ( ￿ 2 ). Thus, an important sim-
plification in this form of Hebbian correlational learning
is that it assumes that the activation variables have zero
mean and unit variance. We will see later that we can
do away with this assumption for the form of Hebbian
learning that we actually use.
The main result in equation 4.6 is that the changes
to the weight from input unit i are a weighted average
over the different input units (indexed by k ) of the corre-
lation between these other input units and the particular
input unit i (figure 4.6). Thus, where strong correla-
tions exist across input units, the weights for those units

(4.4)

￿ w = ￿

We can analyze this sum of weight changes more easily
if we assume that the arbitrary learning rate constant ￿
is equal to ,where N is the total number of patterns

in the input. This turns the sum into an average :

(4.5)

(where the h x i t notation indicates the average or ex-
pected value of variable x over patterns t ).
If we substitute into this equation the formula for y j
(equation 4.1, using the index k to sum over the inputs),