Cryptography Reference
In-Depth Information
3.5.2 Baby-Step Giant-Step Method
The
baby-step giant-step
algorithm is one of the simplest trade-offs on time versus space, in that we are using
some pre-computed values to help us compute the answers we need below.
Baby-Step Giant-Step.
For the following algorithm, assume we are working in finite field over
p
, solving
a
x
=
b
in
p
for
x
.
1. Compute
L
= rounded down, using the normal numerical square root operation.
2. Pre-compute the first
L
powers of a, {
a
1
,
a
2
, ... ,
a
L
}, and store them in a lookup table, indexed by the
exponents {1, 2, 3, ... ,
L
}.
3. Let
h
= (
a
-1
)
L
, our multiplier.
4. Let
t
=
b
, our starting point.
5. For each value of
j
in {0, 1, ... ,
L
- 1}, do the following:
(a) If
t
is in the lookup table (some index
i
exists such that
a
i
=
t
in the field), then return
i
+
j
×
L
.
(b) Set
t
=
t
×
h
.
Basically, we are computing
b
×
h
j
in the loop and terminating when it equals some a
i
, where 0 ≤
i
<
L
, giving
us
Therefore, the discrete logarithm of
b
is
Lj
+
i
.
3.5.2.1 Baby-Step Giant-Step Analysis
The baby-step giant-step algorithm represents a hybrid of the first two brute-force methods. It has on the order
of space requirements (for the
L
powers of
a
) and about log(
p
) running time.
Like the previous brute-force methods, this method will find us an answer eventually, and there is no ran-
domness involved. However, the space requirements are fairly large. For example, when
p
has hundreds or
thousands of digits, then will have roughly half the same number of digits, which will still be hundreds or
thousands of digits! This amount of storage exceeds the capacity of current technology.
3.5.3 Pollard's
ρ
for Discrete Logarithms
Pollard's
ρ
method for discrete logarithms [11] relies on a similar principle as Pollard's
ρ
method for factoring
— that is, we are looking for a cycle when stepping through exponents of random elements.
Here, assume that the group we are working with (the field) is the set of integers between 0 and
ρ
- 1 (written
as
p
) along with normal addition and multiplication.



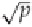

Search WWH ::

Custom Search