Cryptography Reference
In-Depth Information
First, let's learn some new notation. If we wish to convey “x rounded down to the nearest integer,” we can
succinctly denote this using the
floor function
x
. This means that 5.5 = 5, -1.1 = -2 and 3 = 3, for
example. I have avoided using this notation before, but it will be necessary in the following sections.
One more quick definition. A
continued fraction
is a fraction that has an infinite representation. For ex-
ample:
Furthermore, a continued fraction for any number (say,
c)
can be constructed noting that
c
= c +
c
- c ,
or
Let
We stop whenever
c
i
=
C
i
. If not, we continue computing
. After a few steps,
c
looks like
Furthermore, with a continued fraction form like the above (written compactly as [
c
0
,
c
1
, ... ,
c
k
]), we can find
A
k
/
B
k
, the rational number it represents, by the following method:
1. Let
A
-1
= 0,
B
-1
= 1,
A
0
=
c
0
,
B
0
= 1.
2. For each
i
, compute
A
i
=
c
i
A
i
-1 +
A
i
-2 and
B
i
=
c
i
B
i -1
+ B
i
-2.
The above algorithm will eventually terminate if the number being represented is irrational. Otherwise, it
continues forever.
Using this method, we can now compute
quadratic residues,
Q
i
— remainders when subtracting a squared
number. The quadratic residues we are interested in are from
representing the square of
the difference between the form
A
i
/
B
i
and
n
. Taking this formula modulo
n
, we get
We will use the quadratic residues to derive a continued fraction sequence for
where
a
is the number we
wish to factor.
We need an upper-bound on factors we will consider,
B
. The algorithm for exploiting this works by factoring
each
Q
i
as we calculate it, and if it is
B
-smooth (contains no prime factors less than
B
), we record it with the
corresponding
A
i
. After we have collected a large number of these pairs, we look at the exponents of the factors
of each
Q
i
(modulo 2) and find equivalences between them. These will represent a system of equations of the
form:
x
2
≡
y
2
(mod
n
)
When
x
is not equal to
y
, we use the same principle of Fermat's difference of squares to factor
n.







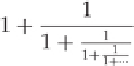



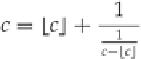
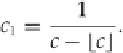


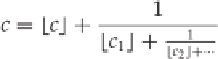



Search WWH ::

Custom Search