Cryptography Reference
In-Depth Information
root as well; two numbers larger than its square root multiplied together will be larger than the number itself!
Therefore, searching up to will be sufficient for finding all the factors.
The only other small trick is the ability to find all of the prime numbers in order to divide by them.
Figure
3-2
shows an example of brute-force factorization using such a list. Although for smaller numbers (only a few
digits), the list of primes needed would be small, it would be prohibitive to have a list of all the prime numbers
required for large factorization lying around. Furthermore, even checking to see if a large number is prime can
be costly (since it would involve a very similar algorithm to that above).
Figure 3-2
Factorization of the number 2431 using brute-force.
The answer is that we would just hop through the list of all integers, skipping ones that are obviously not
primes, like even numbers, those divisible by three, and so forth. For more details on implementations and be-
havior of this algorithm, see Reference [6].
We leave it as an exercise to the reader to implement the brute-force algorithm.
3.3.1.1 Analysis
In order to see how much time this takes to run, we need to know how many prime numbers there are. We could
simply count them, which would be the only exact method. But there is a well-known rough approximation,
saying that if we have a number
a,
then there are approximately
prime numbers less than or equal to
a
. In reality, there are a bit more than this, but this provides a good lower
bound. In terms of the length of
a
(in binary digits), we have
n
= log
2
a
digits.
The running time will then be one division operation per prime number less than the square root of the num-
ber a, which has n/2 digits. Therefore, dividing by every prime number of less than will involve time com-
plexity of about
O
( /log( )), which, when converted to terms of
n
(the number of digits), gives us

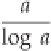

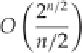
Search WWH ::

Custom Search